分享笑话一则：凌乱之美。

从今天开始，我们就要初涉算法，请大家做好心理准备嗷！

函数

先说说什么是函数。
大家眼里的函数，可能是这个样的：

哈，多么美妙的图案！

实际上，在计算机里，函数是这个样的：

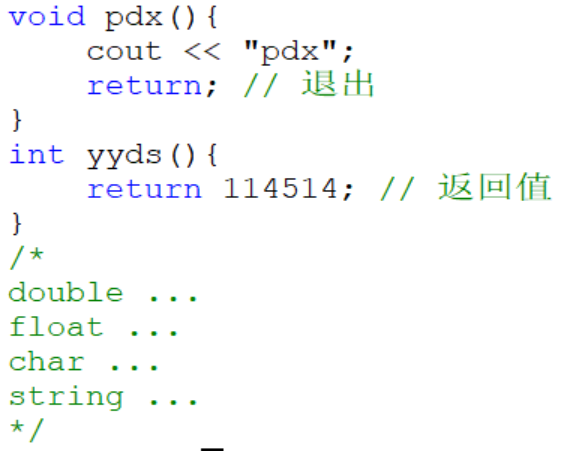
当然，如果复杂一点点，是这样的：

我们以前写的 $main$ 函数，也是一个函数（废话，那必须的啊），你可以按照 $main$ 的写法，写出一个函数：

类型名 函数名(类型1 参数1, 类型2 参数2, ……){ // 也可以不要参数
    你在函数内要做的事儿
    return 返回的类型; // 必须与函数开头那个一样
}

如果不需要返回值，你可以声明 $void$ 类型的函数。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
int c, p, q;
void hahaha(int a, int b){
    c = a+b;
    return; // 退出函数
    c = 0; // 不会执行
}
int main(){
    cin >> p >> q;
    hahaha(p, q);
    cout << c;
    return 0;
}

但你如何退出整个程序呢？$exit(0)$ 。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
int c, p, q;
void hahaha(int a, int b){
	c = a+b;
	exit(0);
}
int main(){
	cin >> p >> q;
	hahaha(p, q);
	cout << c;
	return 0;
}

所以程序不会输出。

递归

递归这个名词大家估计都耳熟能详吧，那咱们跳过吧 但是我们还是要好好学习递归的，因为递归对于我们后面学习深搜、二叉树是非常重要的。

如果你还没听说过递归，那么我告诉你，你可以把递归理解成一种特殊的循环。还记得小时候听过的“老和尚讲故事”吗？讲来讲去，你就陷入了循环，自己讲起了我自己。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
void story(){
    cout << "从前有座山，山上有座庙。庙里有个老和尚给小和尚讲故事，讲的是什么呢？" << endl;
    story(); // 我自己执行我自己
}
int main(){
    story();
    return 0;
}

然后你会发现，控制台上输出了非常多的故事，直到你把它关掉，这就类似于死循环，我们称这种递归叫做无穷递归。
前段时间我们说 $while$ 循环的时候，那个括号里的表达式就是循环条件。如果不满足循环条件， $while$ 循环就会结束，然后继续运行后面的指令。所以我们想让递归结束，必须要设置边界条件，这样就能实现有穷递归。
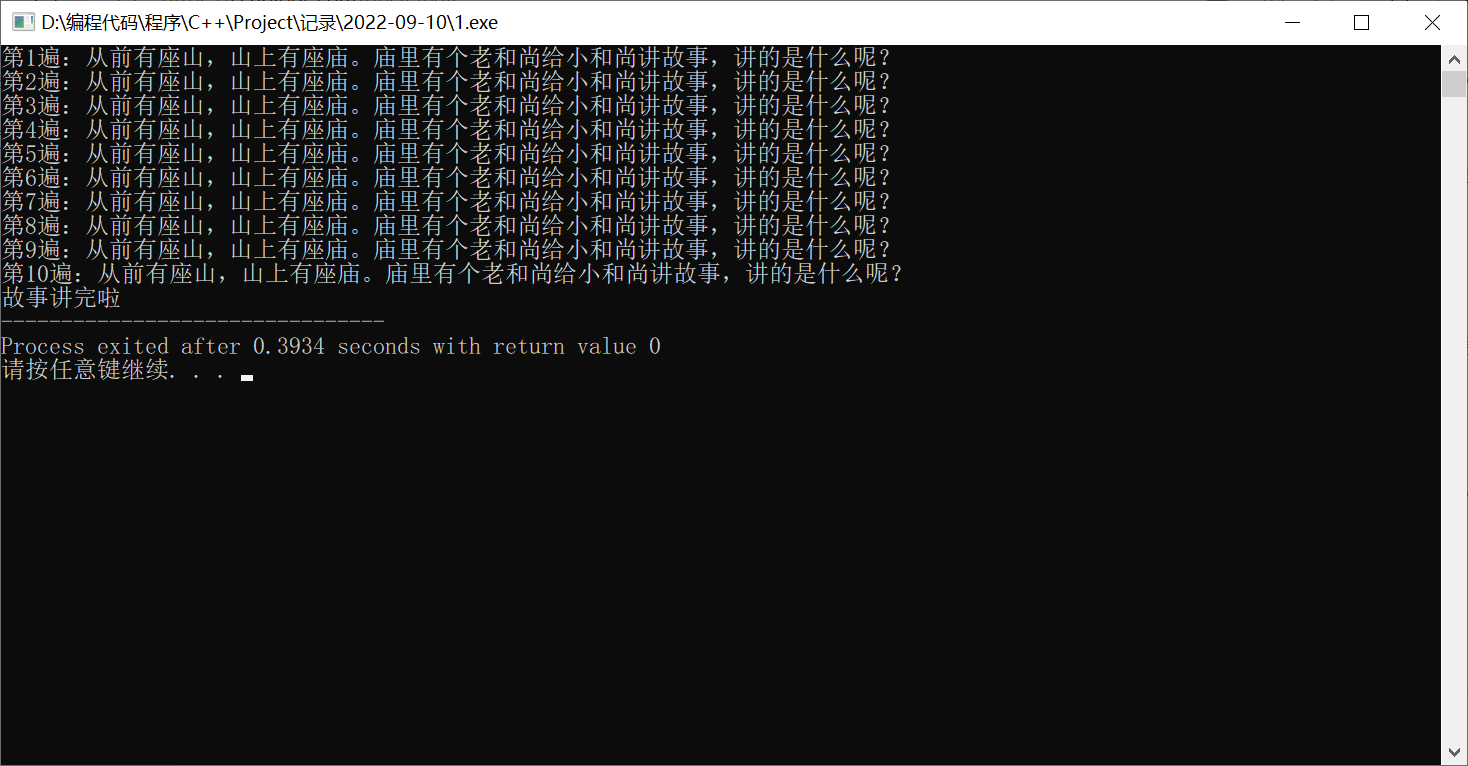
比如说，我们刚才讲故事的例子，如果我们想让程序输出 $10$ 遍，那么该怎么写？

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
void story(int k){ // k 表示故事讲了k遍
    if(k > 10){ // 讲了10遍以上
        printf("故事讲完啦");
        return; // 退出递归
    }
    printf("第%d遍：从前有座山，山上有座庙。庙里有个老和尚给小和尚讲故事，讲的是什么呢？\n", k);
    story(k+1); // 讲了一遍故事
}
int main(){
    story(1); // 从第一遍开始讲故事
    return 0;
}

当然你也可以自由地控制递归次数，要多上机尝试、练习。
我们来做个题儿应用一下吧：

这个题其实用循环也能过，官方给的标签也是循环结构，但是我喜欢用递归解。
程序也并不难，如下：

回溯

可能有的小伙伴一听“回溯”，就吓得不轻：难道你要给我讲深搜？
其实递归的回溯并不难好叭，大家模拟一下就可以咯。

请你阅读以下这个程序，告诉我，结果会输出多少？

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
void f(int k){
    if(k > 5) return;
    printf("%d ", k);
    f(k+1);
    printf("%d ", k);
}
int main(){
    f(1);
    return 0;
}

答案是：

1 2 3 4 5 5 4 3 2 1

为什么会这样？我们来模拟一下。

最开始，主函数调用给进函数的参数 $k=1$。进来以后走流程：

1. 判断：$k$ 如果大于 $5$ 就退出。
2. 输出当前 $k$ 的值；
3. 递归 $k$ 增加 $1$。
4. 递归到边界时，输出 $k$ 的值。

可见如果递归到 $k=5$ 时程序先输出，后面程序尝试递归 $k=6$ 发现：诶，$k>5$ 了，该退出递归了！
退出了递归 $k=6$，程序继续执行当前层数（$k=5$）的后面的命令，输出了 $5$，然后 $k=5$ 的递归结束，继续进行 $k=4$ 的递归……
长此以往， 运行到 $k=1$ 时（又回到了主程序给定的 $k$ 的值时），递归结束。

利用这个特点，我给你出一道题吧。

【角谷猜想的过程】
现在，给你一个数，要求你把角谷猜想（就是上面那个）的过程展现出来。
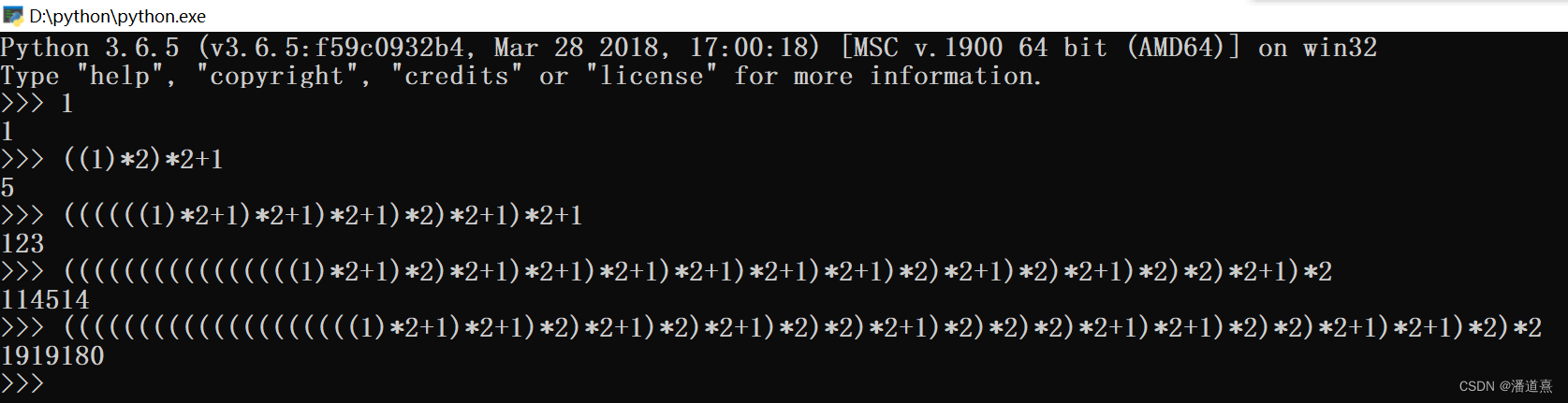
例如：

• 输入 $1$，应该输出：1。
• 输入 $5$，应该输出：((1)*2)*2+1。
• 输入 $123$，应该输出：((((((1)*2+1)*2+1)*2+1)*2)*2+1)*2+1。
• 输入$114514$，应该输出：((((((((((((((((1)*2+1)*2)*2+1)*2+1)*2+1)*2+1)*2+1)*2+1)*2)*2+1)*2)*2+1)*2)*2)*2+1)*2。
• 输入 $1919180$，应该输出：((((((((((((((((((((1)*2+1)*2+1)*2)*2+1)*2)*2+1)*2)*2)*2+1)*2)*2)*2)*2+1)*2+1)*2)*2)*2+1)*2+1)*2)*2。

不信你可以把它还原回去，还是原来那个数。

这个程序，我们可以这么写：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
void f(int k){
    if(k == 1){
        cout << 1;
        return;
    }
    cout << "(";
    bool flag = k&1;
    f(flag ? ((k-1)/2) : (k/2));
    cout << ")*2";
    if(flag) cout << "+1";
}
int main(){
    int n;
    cin >> n;
    f(n);
    return 0;
}

做俩简单的题儿：

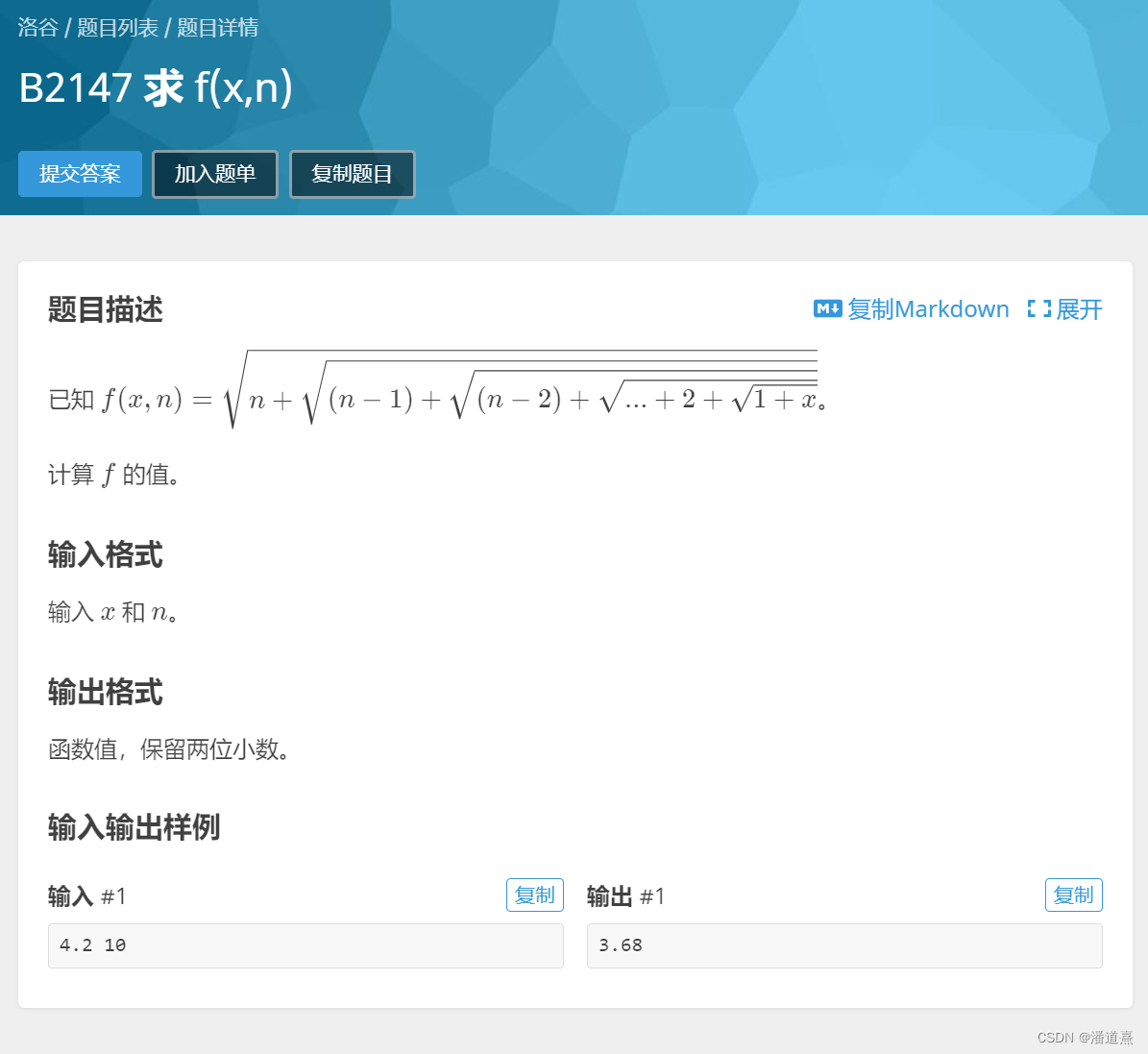
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
double f(double x, int n){
    if(n == 1) return sqrt(1.0 + x);
    return sqrt(n + f(x, --n));
}
int main(){
    double x;
    int n;
    cin >> x >> n;
    cout << fixed << setprecision(2) << f(x, n);
    return 0;
}

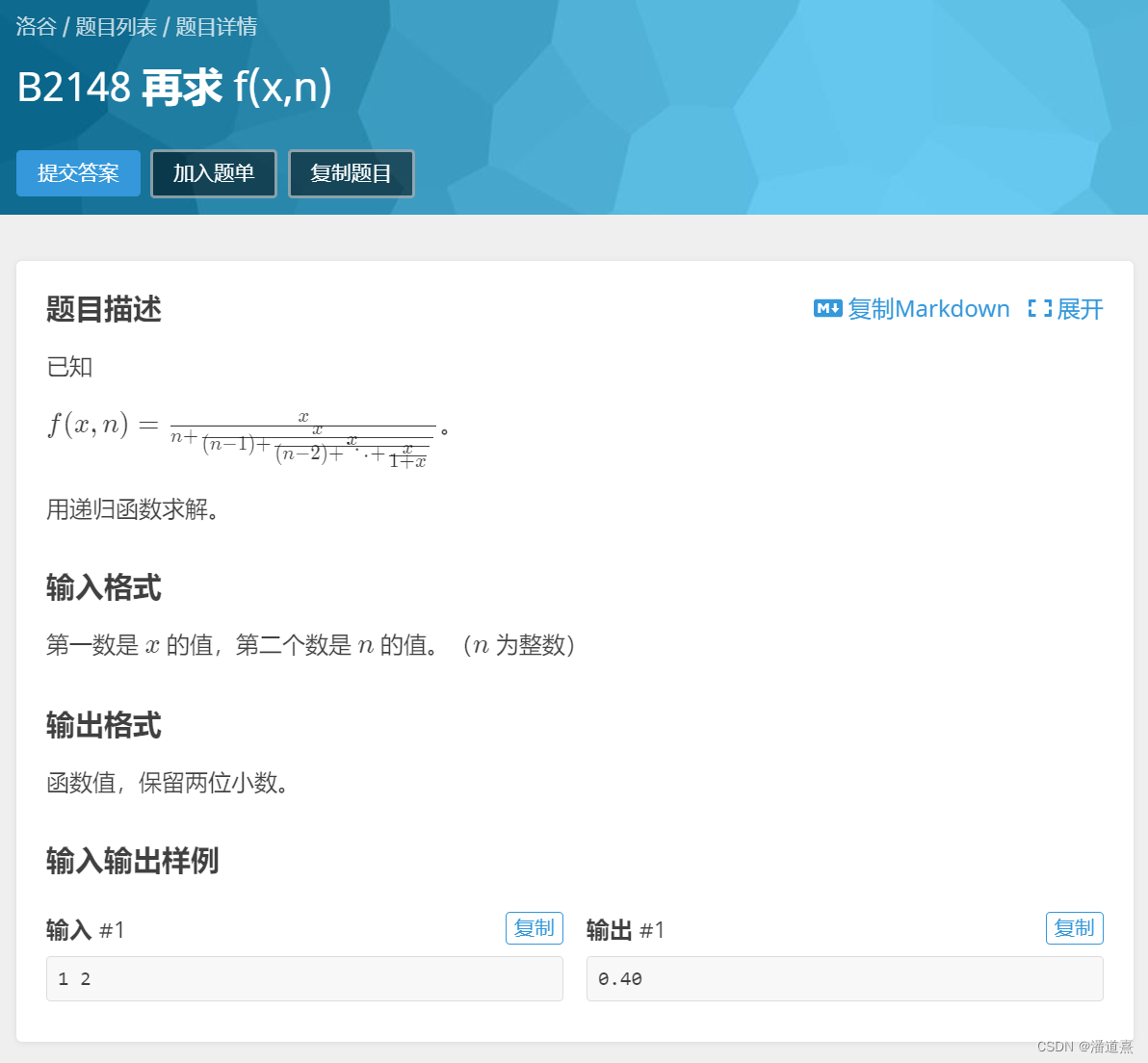
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
double f(double x, int n){
    if(n == 1) return x / (1.0+x);
    return x / (n + f(x, --n));
}
int main(){
    double x;
    int n;
    cin >> x >> n;
    cout << fixed << setprecision(2) << f(x, n);
    return 0;
}

好啦好啦，后面我们就要趁热打铁学深搜了！
我目前的规划是：

• 递归
• 深搜
• 排序
• 贪心
• 递推
• 栈和队列
• 二分
• 广搜
• 动态规划
• …………