众所周知,贪心是从局部最优解推算到全局最优解。
那么 (动态规划)就是枚举出来每一种情况找到最优解。
但是有的时候,初学者无法轻易地推出来递推(状态转移)方程。
我们就容易想到,深搜 同样可以枚举出来每一种结果,
但是,同一个状态会访问多次,时间复杂度呈指数形,大多数情况是 。
今天我介绍一种方式优化上文所述的算法——记忆化搜索。
它可以保证每一个状态只访问一次,基本上与递推同样快。
至少在普及组里可以替代动态规划。
我个人觉得,记忆化的思路、实现远比推方程式简单。
结合例题,来看看如何实现。
【 过河卒】
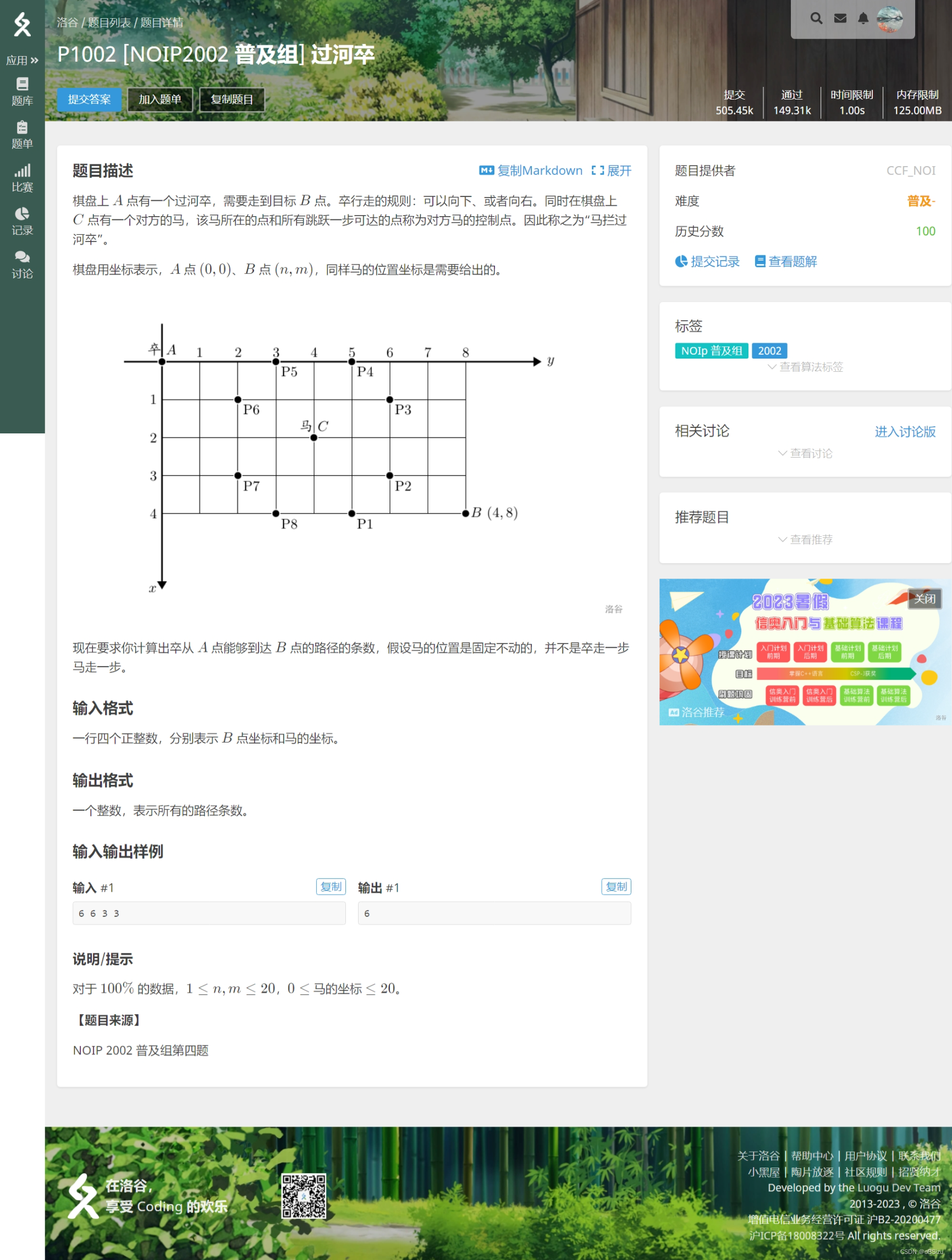
做法
我们知道卒行走的规则是向下或向右,所以一个卒来的方向,要么从上面来,要么从左边来。
令 表示卒可以走到 的路径条数。
我们可以列出方程:
程序也很好实现:
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 51;
ll n, m, cx, cy, a[INF][INF], // a[i][j]: 能从多少条路径走到 (i, j)
// 八面威风
fx[9] = {0, -2, 2, -1, 1, 1, -1, 2, -2},
fy[9] = {0, -1, -1, -2, -2, 2, 2, 1, 1};
int main(){
ios :: sync_with_stdio(0);
cin >> n >> m >> cx >> cy;
for(int i=0; i<=n; i++){
for(int j=0; j<=m; j++){
a[i][j] = 1;
}
}
for(int i=0; i<=8; i++){
// 马可以走到的位置,卒不能走,特殊标记
if(cx+fx[i]>=0 && cx+fx[i]<=n && cy+fy[i]>=0 && cy+fy[i]<=m){
a[cx + fx[i]][cy + fy[i]] = 0;
}
}
for(int i=0; i<=n; i++){
for(int j=0; j<=m; j++){
// 枚举每一个位置
if(!a[i][j] || i==0 && j==0) continue;
else if(i == 0) a[i][j] = a[i][j-1];
else if(j == 0) a[i][j] = a[i-1][j];
else a[i][j] = a[i-1][j] + a[i][j-1];
}
}
cout << a[n][m];
return 0;
}

记忆化搜索
显然,直接搜索肯定会爆炸。我写了暴力 ,都只有 分。
暴力 做法:
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 21;
bool vis[INF][INF];
int n, m, x, y, ans,
fx[3] = {0, 0, 1}, fy[3] = {0, 1, 0},
mx[9] = {0, -2, 2, -1, 1, 1, -1, 2, -2},
my[9] = {0, -1, -1, -2, -2, 2, 2, 1, 1};
bool check(int xx, int yy){
return xx >= 0 && xx <= n && yy >= 0 && yy <= m;
}
void dfs(int x, int y){
if(x == n && y == m){
ans++;
return;
}
for(int i = 1; i <= 2; i++){
int xx = x + fx[i], yy = y + fy[i];
if(check(xx, yy) && !vis[xx][yy]){
dfs(xx, yy);
}
}
}
int main(){
ios :: sync_with_stdio(false);
cin >> n >> m >> x >> y;
for(int i = 0; i <= 8; i++){
int xx = x + mx[i], yy = y + my[i];
if(check(xx, yy)){
vis[xx][yy] = true;
}
}
dfs(0, 0);
cout << ans;
return 0;
}
于是我在深搜基础上加了个记忆化:
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
// 懒人方法
#define int long long
const int INF = 21;
bool vis[INF][INF]; // vis[i][j]: 记录是否访问过 (i, j)
int n, m, x, y, f[INF][INF], // f[i][j]: 记忆化数组,从 (i, j) 可以有多少条路线到达终点
fx[3] = {0, 0, 1}, fy[3] = {0, 1, 0}, // 卒行走规则
mx[9] = {0, -2, 2, -1, 1, 1, -1, 2, -2}, // 马行走规则
my[9] = {0, -1, -1, -2, -2, 2, 2, 1, 1};
bool check(int xx, int yy){ // 判断是否越界
return xx >= 0 && xx <= n && yy >= 0 && yy <= m;
}
int dfs(int x, int y){
if(x == n && y == m) return f[x][y] = 1; // 到达终点了
if(f[x][y] != -1) return f[x][y]; // 当前已经访问过了,直接输出当时访问的结果
int sum = 0;
for(int i = 1; i <= 2; i++){
int xx = x + fx[i], yy = y + fy[i];
if(check(xx, yy) && !vis[xx][yy]){
sum += dfs(xx, yy);
}
if(vis[xx][yy]) f[xx][yy] = 0; // 这里不能走或者走过了,标记为 0
}
return f[x][y] = sum; // 保存当前结果
}
signed main(){
ios :: sync_with_stdio(false);
cin >> n >> m >> x >> y;
memset(f, -1, sizeof(f)); // 初始化记忆化数组
for(int i = 0; i <= 8; i++){
int xx = x + mx[i], yy = y + my[i];
if(check(xx, yy)){
vis[xx][yy] = true;
f[xx][yy] = 114514; // 标记不能走
}
}
cout << dfs(0, 0);
return 0;
}

甚至跑的比 快!(大喜)
【 数字三角形】
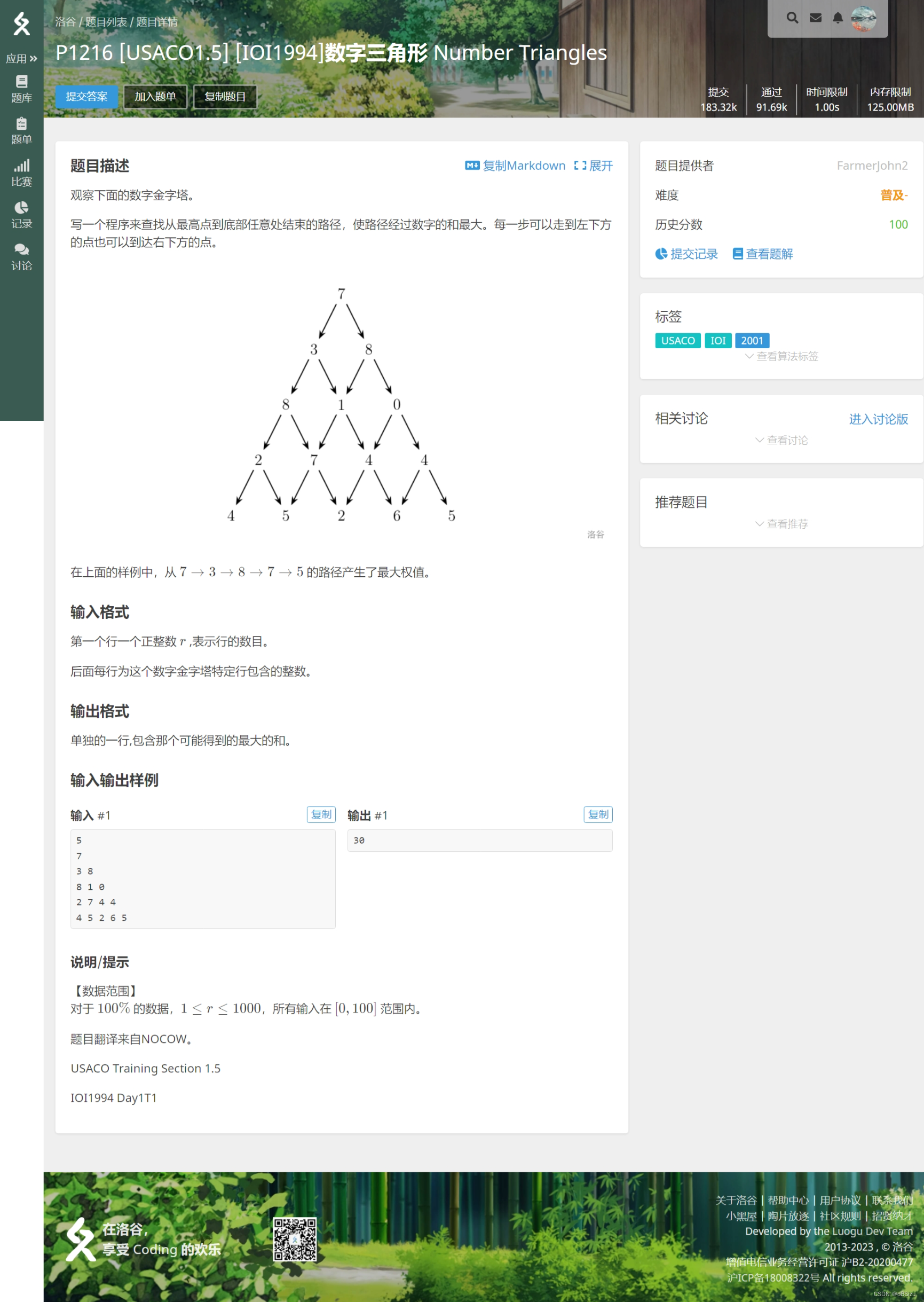
此题堪称经典,是 或递推的板子。
做法
对于每一个数字的位置 ,都可以从 或 的位置加下来。
从数字三角形的最上方顶点开始加,每次都加最大的,最后底边上的最大值就是答案。
也可以从底边的每一个数往上加,同理。方程:
程序:
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 1e3 + 1;
int n, a[INF][INF];
int main(){
ios :: sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
cin >> a[i][j];
}
}
for(int i = n-1; i >= 1; i--){
for(int j = 1; j <= i; j++){
a[i][j] += max(a[i+1][j], a[i+1][j+1]);
}
}
cout << a[1][1];
return 0;
}

记忆化搜索
同样,我咔咔咔先打了个暴搜:
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 1e3 + 1;
int n, ans, a[INF][INF];
int dfs(int i, int j, int st = 0){
if(i == n) return st + a[i][j];
return max(max(dfs(i+1, j, st+a[i][j]), dfs(i+1, j+1, st+a[i][j])), st + a[i][j]);
}
int main(){
ios :: sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
cin >> a[i][j];
}
}
ans = INT_MIN;
cout << dfs(1, 1);
return 0;
}
一定会超时的,不用试。
所以我加上记忆化:
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 1e3 + 1;
int n, a[INF][INF], f[INF][INF];
int dfs(int i, int j){
if(f[i][j] != -1) return f[i][j]; // 访问过了
if(i == n) return f[i][j] = a[i][j];
else return f[i][j] = max(dfs(i+1, j), dfs(i+1, j+1)) + a[i][j];
}
int main(){
ios :: sync_with_stdio(false);
memset(f, -1, sizeof(f)); // 初始化
cin >> n;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
cin >> a[i][j];
}
}
cout << dfs(1, 1);
return 0;
}
然后就顺利 了。

为什么会比 慢呢?
搜索是一个递归的过程。我们找到最终的结果后,耗时和递推一样。
但是递归还要归回来,这个过程耽误了时间。
【 榨取 】
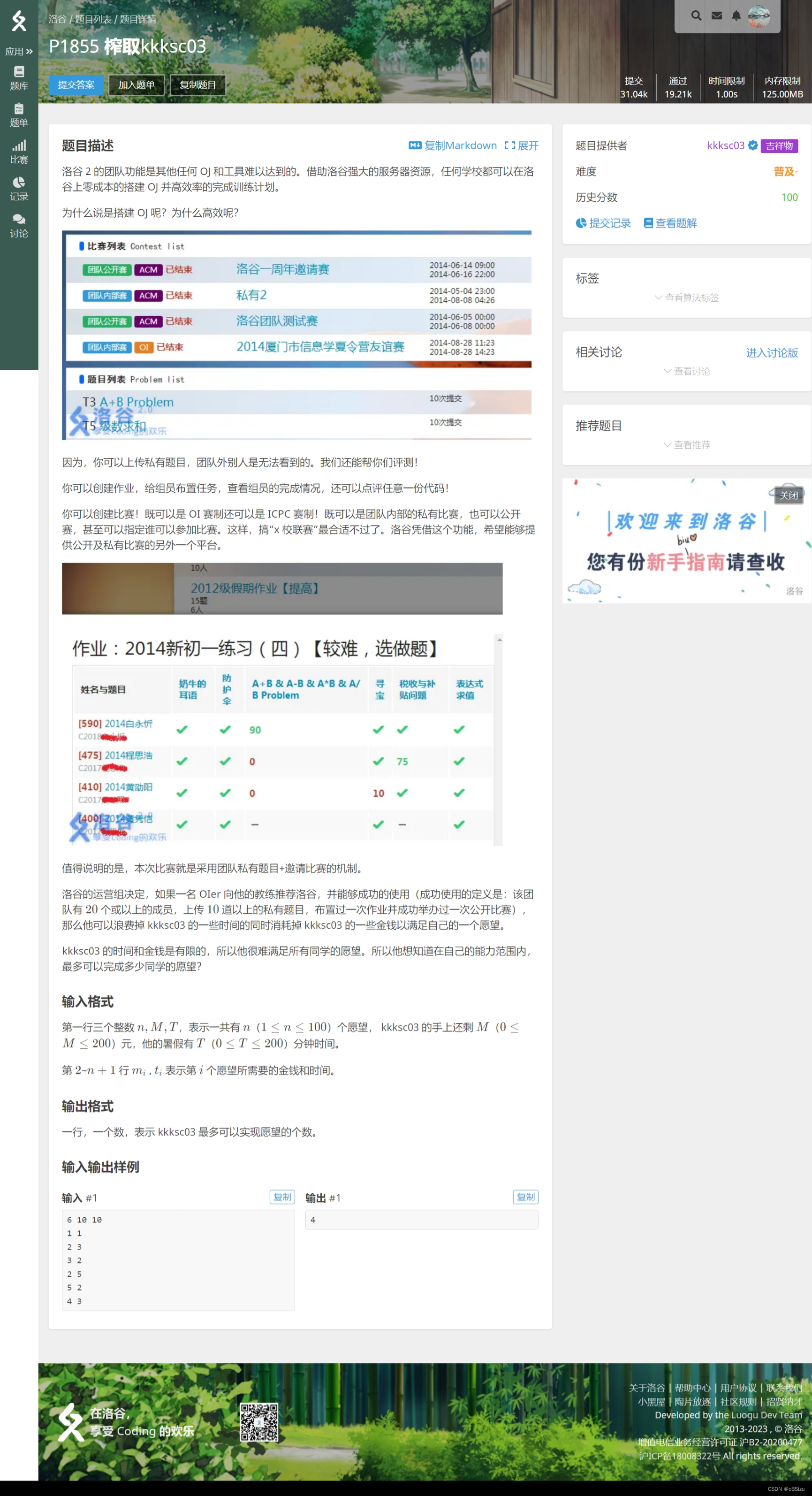
此题很明显是一个背包问题,还是一个多维与 的合体。
做这件事的时间和金钱都是体积,站长的时间和金钱是背包的容积。
所以,如果我不想写递推,就:
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 201;
int n, m, t, f[INF][INF][INF];
struct node {int m, t;} a[INF];
int dfs(int id, int leftM, int leftT){
/*
id: 函数应该处理第 id 件事
leftM: 站长还剩下的钱
leftT: 站长还剩下的时间
*/
if(id == n + 1) return f[id][leftM][leftT] = 0; // 越界,不存在这件事
if(leftM < 0 || leftT < 0) return -1; // 站长没钱或者没时间了,啥事也做不了了
if(leftM < a[id].m || leftT < a[id].t) return f[id][leftM][leftT] = dfs(id + 1, leftM, leftT); // 剩下的时间和钱不够做这件事,那就看看下一件事
if(f[id][leftM][leftT] != -1) return f[id][leftM][leftT]; // 记忆化
int dfs1 = dfs(id + 1, leftM, leftT), // 不做这个事
dfs2 = dfs(id + 1, leftM - a[id].m, leftT - a[id].t) + 1; // 做了,站长做的事增加一个
return f[id][leftM][leftT] = max(dfs1, dfs2); // 哪个能干最多的事儿
}
int main(){
ios :: sync_with_stdio(false);
memset(f, -1, sizeof(f));
cin >> n >> m >> t;
for(int i = 1; i <= n; i++){
cin >> a[i].m >> a[i].t;
}
cout << dfs(1, m, t); // 从第一件事儿开始处理,时间和金钱都是满的
return 0;
}

摆渡车】
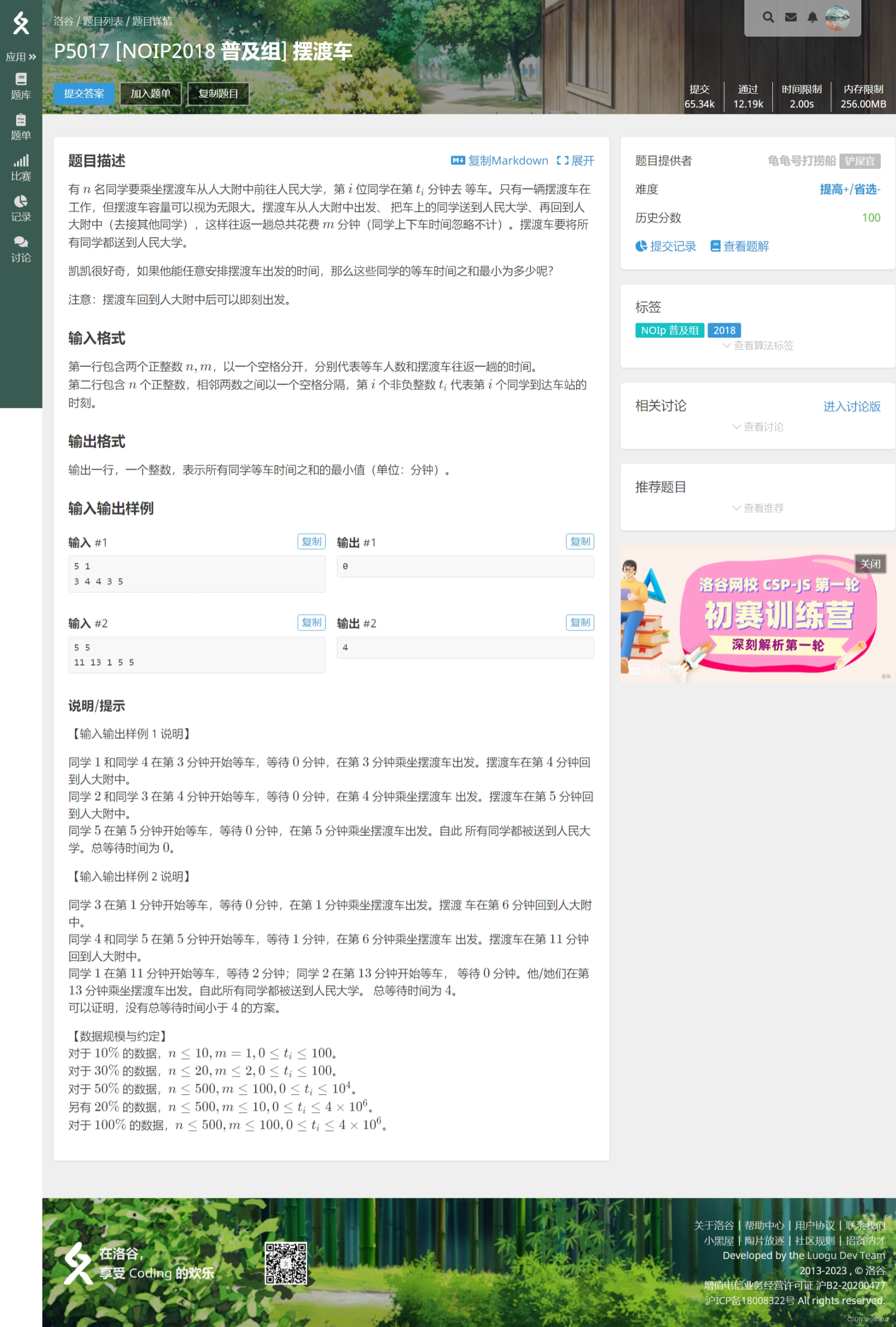
史上最难的一届普及组。
您可以琢磨琢磨程序的写法。
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 501;
int n, m, a[INF], f[INF][INF];
int dfs(int k, int t){
if(k == n + 1) return 0;
if(a[k] > t) return dfs(k, a[k]);
if(f[k][t-a[k]] != -1) return f[k][t-a[k]];
int tmp = 0, j = k;
for(int i = k; i <= n && a[i] <= t; j = ++i){
tmp += a[i];
}
int ans = t * (j-k) - tmp + dfs(j, t+m);
for(int i = j; i <= n; i++){
tmp += a[i];
ans = min(ans, (a[i] * (i-k+1) - tmp + dfs(i+1, a[i]+m)));
}
return f[k][t-a[k]] = ans;
}
int main(){
ios :: sync_with_stdio(false);
memset(f, -1, sizeof(f));
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
sort(a + 1, a + n + 1);
cout << dfs(1, 0);
return 0;
}