好长时间没有写过这个系列了，中间还进行了文章的大迁移，希望大家还记得我。

那么，我们前面说过，递归是深搜的实现过程。递归是什么来着？ 其实就是自调用的函数。

我们不妨假想：对某个问题的答案进行枚举，要做到不重不漏，有什么办法呢？

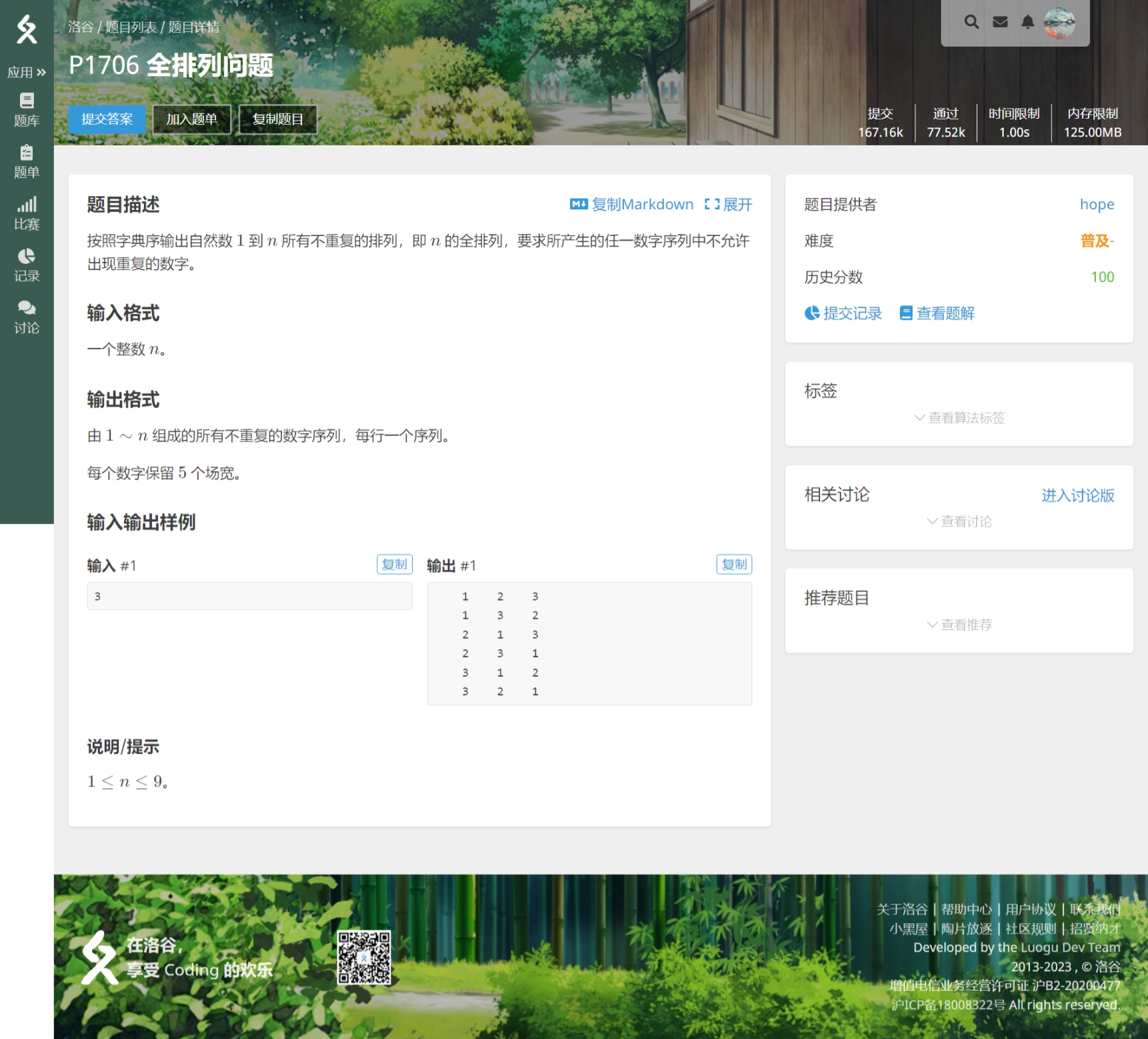
• 全排列问题
• 图论中的深搜问题
• 连通块问题
• 迷宫问题
• 记忆化搜索

全排列问题

三个不同的苹果要放到三个不同的盘子里，不能有空盘子。求放法？

显然，可以列一个表格去做。

方案/盘子	甲	乙	丙
①	$A$ 苹果	$B$ 苹果	$C$ 苹果
②	$A$ 苹果	$C$ 苹果	$B$ 苹果
③	$B$ 苹果	$A$ 苹果	$C$ 苹果
④	$B$ 苹果	$C$ 苹果	$A$ 苹果
⑤	$C$ 苹果	$A$ 苹果	$B$ 苹果
⑥	$C$ 苹果	$B$ 苹果	$A$ 苹果

综上，共 $C^3_3=\frac{3!}{(3-2)!}=6$ 种方案。

对于上面的例子，我们完全可以暴力，程序如下：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

#define endl "\n"
#define ll long long

const int INF = 4; 		// 三个苹果
char pl[INF]; 			// 盘子里放的什么苹果
map <char, bool> vis;  	// 标记苹果是否已经放入盘里（只能用一次）

int main(){
	ios :: sync_with_stdio(false);

	for(char i='A'; i<='C'; i++){ // 枚举第一个苹果
		pl[1] = i; // 记录下第一个盘子放的苹果 i
		vis[i] = true; // 标记已使用
		for(char j='A'; j<='C'; j++){ // 枚举第二个苹果
		    if(vis[j]) continue; // 如果已经使用过，就跳过
			pl[2] = j;
			vis[j] = true;
			for(char k='A'; k<='C'; k++){ // 枚举第三个苹果
				if(vis[k]) continue;
				pl[3] = k;
				vis[k] = true;
				cout << i << " " << j << " " << k << endl; // 输出苹果方案
				vis[k] = false;
			}
			vis[j] = false; // 拿出来苹果，再继续放
		}
		vis[i] = false;
	}

	return 0;
}

很麻烦，中间很多东西都是来回判断，对不对？

而且此程序还有一个致命的缺陷，如果有 $n$ 个苹果和 $n$ 个盘子，就没办法这样一个个写循环了，除非一个个判断（显然不现实）。

对于这个缺陷，我们可以使用递归的思想去作答——该如何考虑呢？

这，就是经典的深度优先搜索——全排列问题。

$\text{DFS}$ 全称是 $\text{Depth First Search}$，中文名是深度优先搜索，是一种用于遍历或搜索树或图的算法。所谓深度优先，就是说每次都尝试向更深的节点走。——$\text{OI Wiki}$

我们可以每次都枚举当前这一步放什么苹果，接着再下一步……知道发现结果。

根据这个原理，我们可以写下一个简单的深搜：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

#define endl "\n"
#define ll long long

const int INF = 11; 		
int n;                  // 多个苹果（A、B、C、D……）
char pl[INF]; 			// 盘子里放的什么苹果
map <char, bool> vis;  	// 标记苹果是否已经放入盘里（只能用一次）

void dfs(int st){         	// st 当前该放哪个盘子了
	if(st == n+1){ 			// 若 n 个苹果都枚举到了
		for(int i=1; i<=n; i++){ // 输出
			cout << pl[i] << " \n"[i == n];
		}
		return;         	// 边界条件
	}
	for(int i=1; i<=n; i++){ 		    // 一个个地试
		char c = 'A' + i - 1;           // c 苹果的编号
		if(!vis[c]){         		    // 若当前苹果没被用过
			pl[st] = c;                 // 放进盘子
			vis[c] = true;              // 标记这个苹果用过了
			dfs(st + 1);                // 接着枚举下一个盘子的情况
			vis[c] = false;             // 把苹果拿出来（回溯）
		}
	}
}

int main(){
	ios :: sync_with_stdio(false);

	cin >> n;
	dfs(1); 				// 从第一个苹果开始枚举
	
	return 0;
}

一定一定要理解这段程序！！

（等待中）

简单的全排列问题，相信你已经完全理解了吧！

// Author:PanDaoxi
// 我承认，当时的码风足够丑……这是我新的码风形成初期写的
#include <bits/stdc++.h>
using namespace std;
const int inf = 10;
int n, use[inf];
bool vis[inf]; // 标记使用过

void dfs(int k){
	if(k == n){
		// 输出
		for(int i=1; i<=n; i++){
			printf("%5d", use[i]);
		}
		printf("\n");
		return;
	}
	for(int i=1; i<=n; i++){
		if(!vis[i]){
			vis[i] = true; //标记使用过
			use[k+1] = i;
			dfs(k+1); // 递归
			// 回溯
			vis[i] = false;
		}
	}
}

int main(){
	cin >> n;
	dfs(0); // 开始递归
	return 0;
}

图论中的深搜问题

我们刚刚说全排列中的深搜，是逐个判断当前这一位的情况是否可行，直到全部填满。

树是一种特殊的图，其特点是一个前驱，多个后继。对于树的储存方法，我们已经讲过，可以通过父亲表示法，也可以通过孩子表示法，用链表存储即可。遍历的方式一共四种：先序遍历（先根遍历，根左右）、中序遍历（左根右）、后序遍历（后根遍历，左右根）、层序遍历（宽度优先搜索 $\text{BFS}$）。

那么，我现在给出一个有子权的无向连通图，有四个结点，共六条路径。

从 $v_0$ 走到 $v_3$ 一共有多少不同路径？

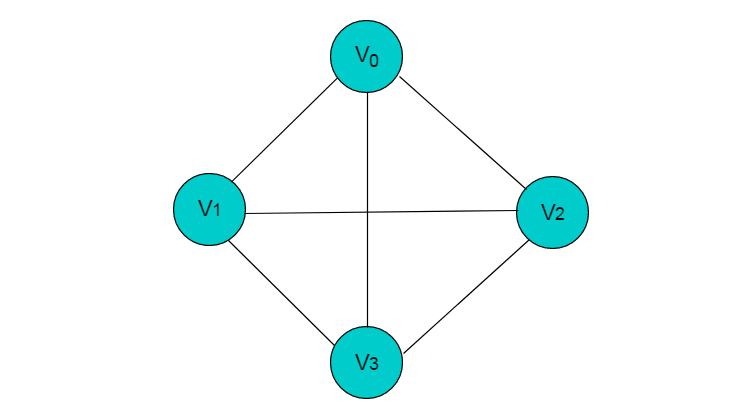
我们首先考虑如何存储图。对于这类问题，可以使用邻接矩阵。即：

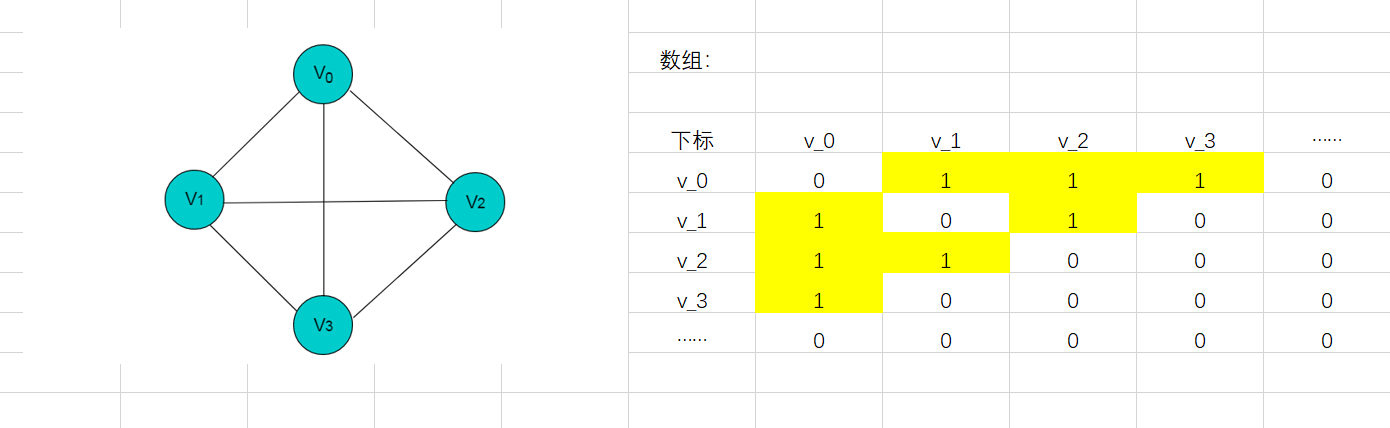
可以走的地方写成真，不能走的地方写成假。

……具体的程序和理解，可以参考这篇文章。图论的知识点，后期会单独开一章来讲。

连通块问题

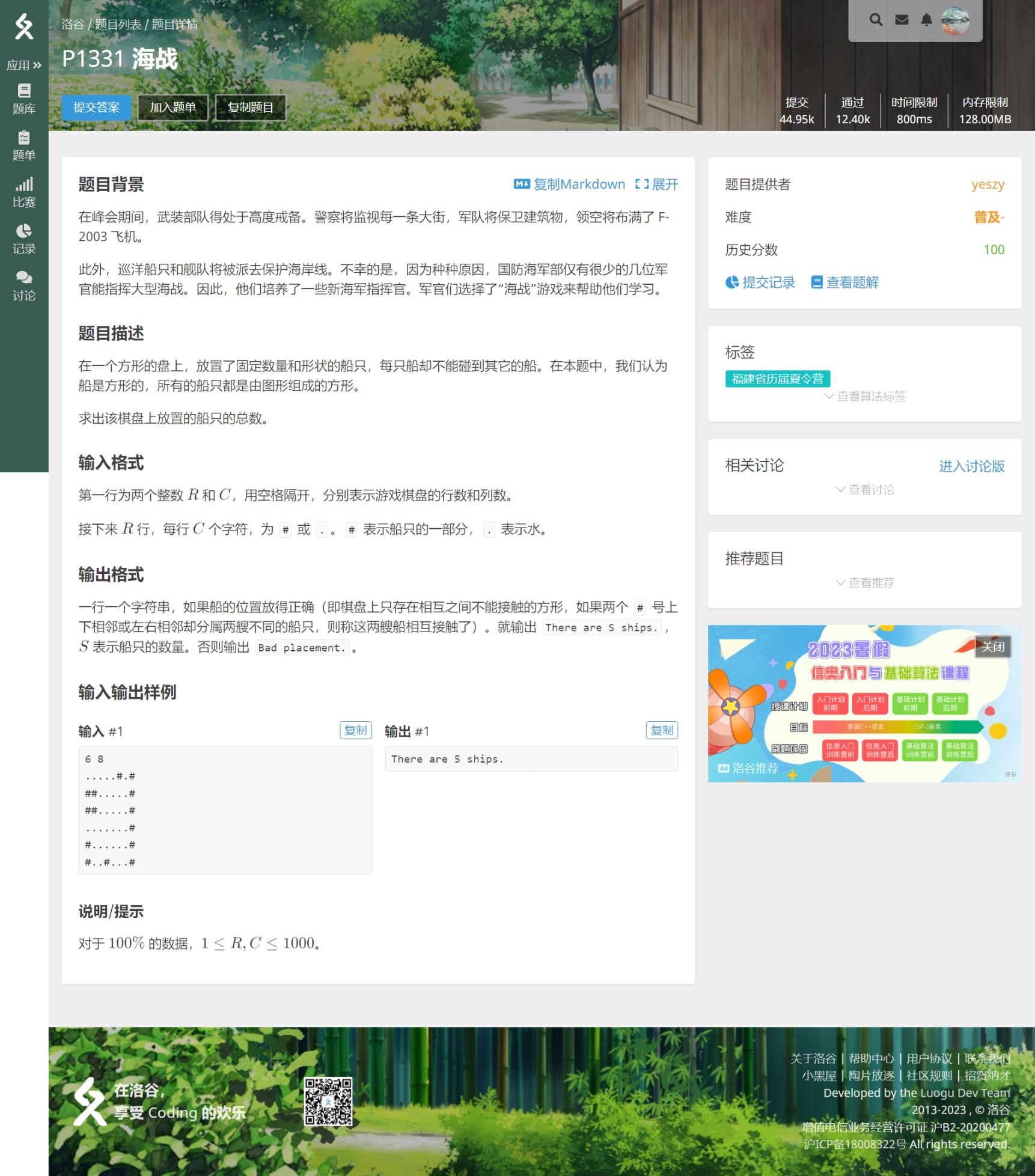
这道题是很经典的连通块问题。连通块，即上下左右相连的字符。

——可以用深搜去查看任意的一个 #，在搜索时寻找相同的符号，进入时将其标记为其他东西，并且计数器增加。这种办法，叫做洪水填充法。

最后，如何判断是否为矩形？

维护一个最小坐标和一个最大坐标，相减后可以得到矩形的长和宽，再判断是否等于当前连通块 # 的总数即可。

完整程序：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
const int inf = 1e3 + 1;
int n, m, ans, cnt, maxi, maxj, mini, minj,
	fx[5] = {0, -1, 1, 0, 0},
	fy[5] = {0, 0, 0, -1, 1};
bool a[inf][inf];

void dfs(int x, int y){
	maxi = max(x, maxi),
	maxj = max(y, maxj),
	mini = min(x, mini),
	minj = min(y, minj),
	cnt++, a[x][y] = false;
	
	for(int i=1; i<=4; i++){
		int xx = x + fx[i],
			yy = y + fy[i];
		if(a[xx][yy] && xx >= 1 && x <= n && yy >= 1 && yy <= m){
			dfs(xx, yy);
		}
	}
}

int main(){
	cin >> n >> m;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			char c;
			cin >> c;
			a[i][j] = c == '#';
		}
	}
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			if(a[i][j]){
				cnt = 0,
				maxi = mini = i,
				maxj = minj = j;
				
				dfs(i, j);
				if((maxi-mini+1)*(maxj-minj+1) == cnt){
					ans++;
				}
				else{
					printf("Bad placement.");
					return 0;
				}
			}
		}
	}
	printf("There are %d ships.", ans);
	return 0;
}

高端的应用：染色块。

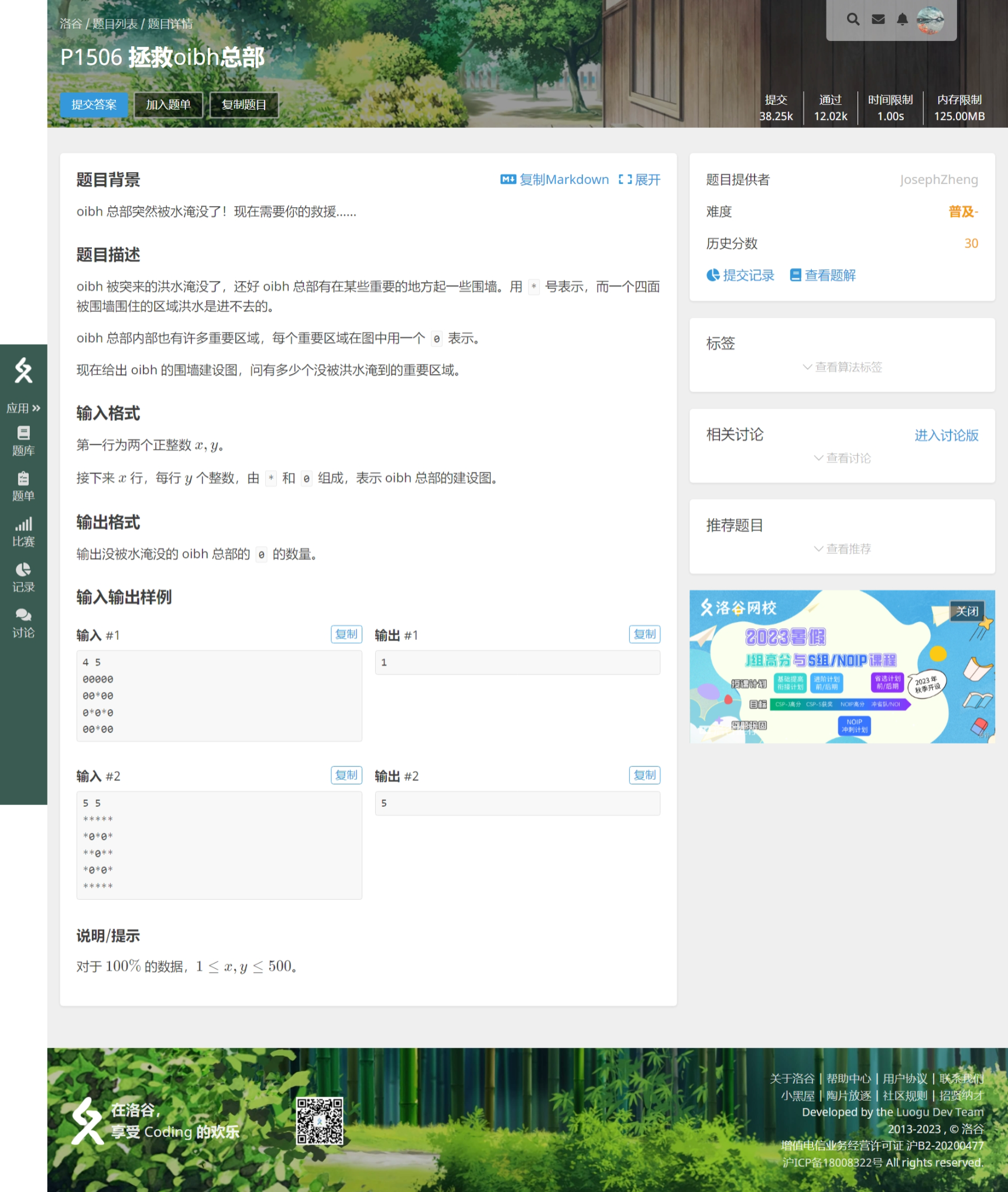
这道题也是一个连通块。我们该怎么完成呢？

我们首先应该区分的开闭合圈外和闭合圈内。

我们完全可以按照刚才的方式，计算数量。

很轻松，写出来一段程序：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

#define endl "\n"
#define ll long long

const int INF = 501;
int n, m, ans, fx[5] = {0, -1, 1, 0, 0}, fy[5] = {0, 0, 0, -1, 1};
char c[INF][INF];

void dfs(int x, int y){
	c[x][y] = '*';
	for(int i=1; i<=4; i++){
		int xx = x + fx[i], yy = y + fy[i];
		if(xx>=1 && xx<=n && yy>=1 && yy<=m && c[xx][yy]=='0'){
			dfs(xx, yy);
		}
	}
}

int main(){
	ios :: sync_with_stdio(false);

    cin >> n >> m;
    for(int i=1; i<=n; i++){
    	for(int j=1; j<=m; j++){
    		cin >> c[i][j];
		}
	}
	dfs(1, 1);
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			if(c[i][j] == '0') ans++;
		}
	}
	cout << ans;

	return 0;
}

交上去一看：

满江红，听取 WA 声一片。

为什么？错误出在了哪里？

我们没有考虑到边界前的连通块无法被填充。有一组 $\text{Hack}$ 数据：

输入：
3 3
**0
*0*
0**

正确的输出：
1

程序的输出：
3

所以，我们需要构造一个连通块，使周围所有都成为一个连通块再填充，就可以填充完整。

这里采用将上下左右的行和列也算进来，构造出一个大闭合圈，填充后，为填充到的部分就是小闭合圈内的安全部分。

正确的程序如下：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

#define endl "\n"
#define ll long long

const int INF = 501;
int n, m, ans, fx[5] = {0, -1, 1, 0, 0}, fy[5] = {0, 0, 0, -1, 1};
char c[INF][INF];

void dfs(int x, int y){
	c[x][y] = '*';
	for(int i=1; i<=4; i++){
		int xx = x + fx[i], yy = y + fy[i];
		if(xx>=0 && xx<=n+1 && yy>=0 && yy<=m+1 && c[xx][yy]=='0'){
			dfs(xx, yy);
		}
	}
}

int main(){
	ios :: sync_with_stdio(false);

    cin >> n >> m;
    for(int i=0; i<=n+1; i++){
    	for(int j=0; j<=m+1; j++){
    		c[i][j] = '0';
			if(i>=1 && i<=n && j>=1 && j<=m) cin >> c[i][j];
		}
	}
	dfs(0, 0);
	for(int i=0; i<=n+1; i++){
		for(int j=0; j<=m+1; j++){
			if(c[i][j] == '0') ans++;
		}
	}
	cout << ans;

	return 0;
}

有一个相似的题目：

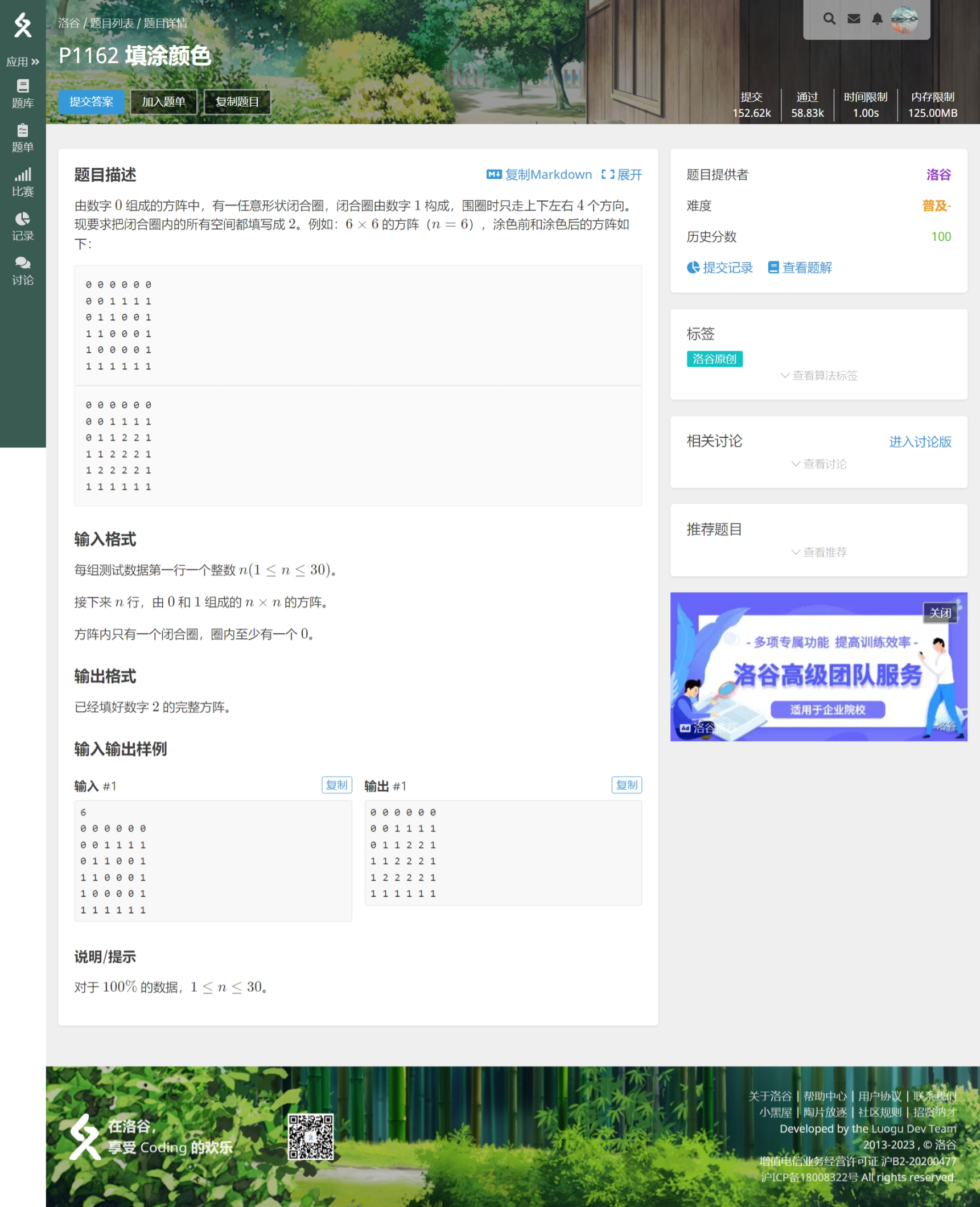
正确的程序如下：

// Author:PanDaoxi 
#include <bits/stdc++.h>
using namespace std;

const int INF = 31;
int n, a[INF][INF],
	fx[5] = {0, -1, 1, 0, 0},
	fy[5] = {0, 0, 0, -1, 1};
bool vis[INF][INF];

void dfs(int x, int y){
	vis[x][y] = true;
	for(int i=1; i<=4; i++){
		int xx = x + fx[i], yy = y + fy[i];
		if(xx>=0 && xx<=n+1 && yy>=0 && yy<=n+1 && !a[xx][yy] && !vis[xx][yy]) dfs(xx, yy);
	}
}

int main(){
	ios :: sync_with_stdio(0);
	
	cin >> n;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			cin >> a[i][j];
		}
	}
	dfs(0, 0);
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			if(!vis[i][j]){
				if(a[i][j] == 1) cout << 1 << " ";
				else cout << 2 << " ";
			}
			else cout << 0 << " ";
		}
		cout << endl;
	}
	
	return 0;
}

注意加深理解！！

迷宫问题

迷宫问题也是深搜的经典问题之一。

根据深搜“不撞南墙不回头”的特点，我们可以让程序像个路痴一样来回跑，能跑到终点就跑到终点，跑到死胡同里再折回来选另一条路。

完全可以遍历到迷宫的每一条路！

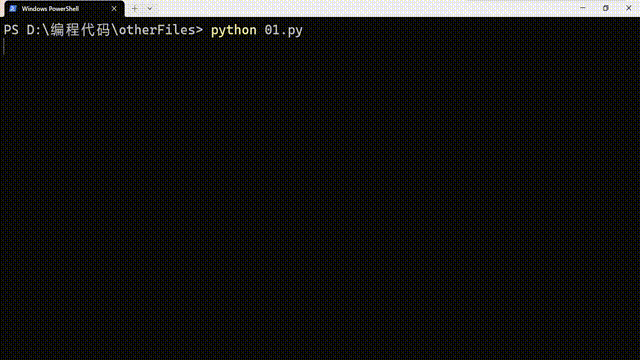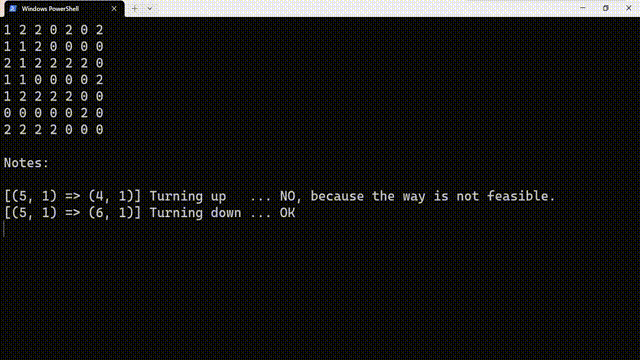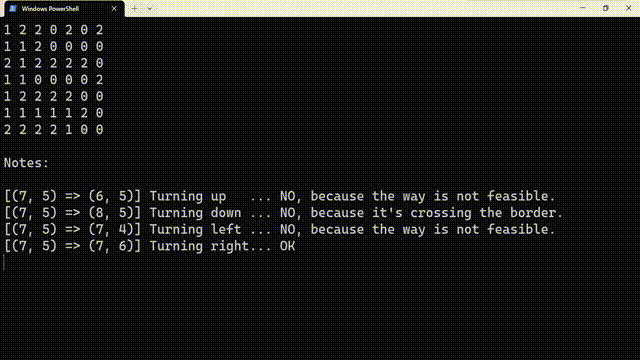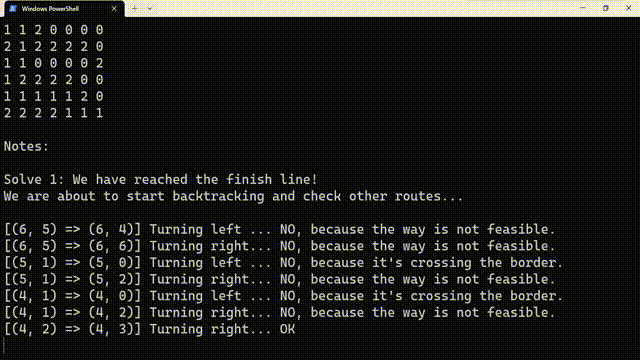
上面的程序是 $\text{Python}$ 实现的深搜迷宫问题模拟器，源代码如下：

（不重要，不想看的可以直接忽略）

（$\text{Python}$ 语法糖太多了，且 $\text{CCF}$ 不认可，所以不用太在意）

# Author:PanDaoxi 
from time import sleep
from os import system

INF, n, ans = 8, 7, 1
f, fx, fy = [
        [0, 0, 0, 0, 0, 0, 0, 0,], 
        [0, 0, 2, 2, 0, 2, 0, 2,],
        [0, 0, 0, 2, 0, 0, 0, 0,],
        [0, 2, 0, 2, 2, 2, 2, 0,],
        [0, 0, 0, 0, 0, 0, 0, 2,],
        [0, 0, 2, 2, 2, 2, 0, 0,],
        [0, 0, 0, 0, 0, 0, 2, 0,],
        [0, 2, 2, 2, 2, 0, 0, 0,],
    ], [0, -1, 1, 0, 0,], [0, 0, 0, -1, 1]

def tprint(i, x, y, xx, yy):
    fl = [0, "up   ", "down ", "left ", "right"]
    if xx >= 1 and xx <= n and yy >= 1 and yy <= n:
        if f[xx][yy] == 0:
            tmp = "OK"
        else:
            tmp = "NO, because the way is not feasible."
    else:
        tmp = "NO, because it's crossing the border." 
    print("[(%d, %d) => (%d, %d)] Turning %s..." % (x, y, xx, yy, fl[i]), tmp)
    return tmp == "OK"

def dfs(x, y, starter = False):
    global ans
    f[x][y] = 1
    if not starter:
        sleep(1)
    system("cls")
    for i in range(1, n+1):
        for j in range(1, n+1):
            print(str(f[i][j]), end=" \n"[j == n])
    print("\nNotes:\n")
    if x == n and y == n:
        f[n][n] = 0
        print("Solve %d: We have reached the finish line!\nWe are about to start backtracking and check other routes...\n" % ans)
        sleep(3)
        ans += 1
        return
    for i in range(1, 5):
        xx, yy = x + fx[i], y + fy[i]
        tmp = ""
        if(tprint(i, x, y, xx, yy)):
            dfs(xx, yy)
        sleep(0.75)

dfs(1, 1, True)
print("\nDFS is completed!")
if ans == 1:
    print("There isn\'t a solve.")

可以试着修改一下。

同样的，在 $\text{C++}$ 中，我们解决迷宫问题的一般步骤为：

• 确定搜索方向
• 确定起点和终点
• 逐个点递归地枚举各个方向的路线
• 记录解

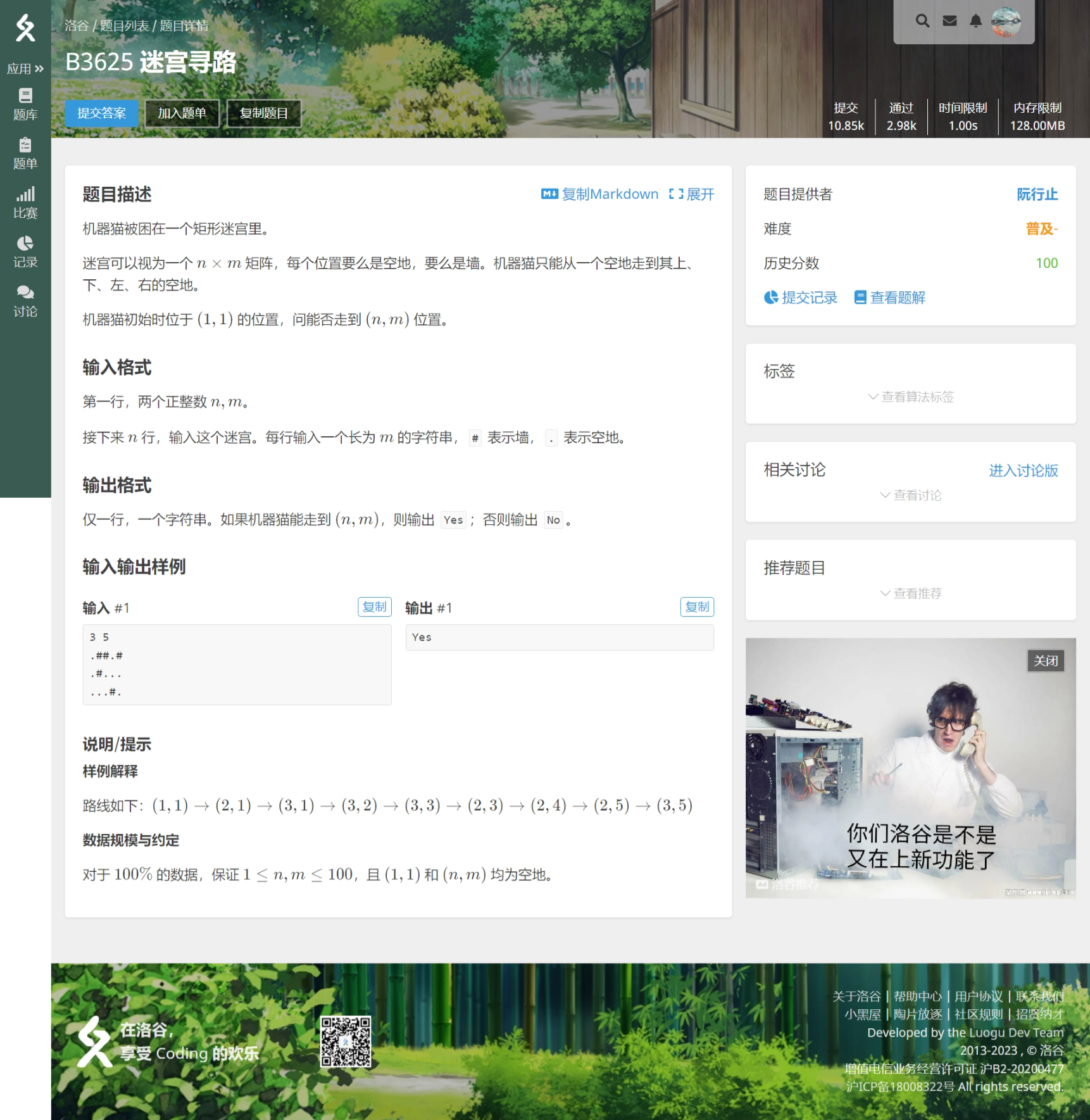
所以，我们在这道题中可以分析出：

• 搜索方向：上下左右或其他，均可。

  储存的时候可以利用数组：

  int fx[5] = {0, -1, 1, 0, 0},
  	fy[5] = {0, 0, 0, -1, 1};
  

  这样通过当前的坐标位置分别加上数组中同一位置的数就可以实现方向的枚举，即：

  for(int i=1; i<=4; i++){
  	newX = oldX + fx[i]; // 这里不建议 x1 y1 一类的，会和 bits/stdc++.h 冲突，产生莫名其妙的错误
  	newY = oldY + fy[i];
  	// 处理和递归
      // ……
  }
  

• 确定起点和终点：题目中明确给出了起点和终点。

  我们在搜索函数里将到达终点作为递归边界，一旦找到到达终点的路线就立即退出程序（此题中没必要继续搜索了）。

  void dfs(int x, int y){
      if(x == n && y == m){
          // 输出
          // ……
          exit(0); // 退出程序
      }
  }
  

• 枚举路线：避开墙、不能越界。

  if(xx>=1 && xx<=n && yy>=1 && yy<=m && a[xx][yy]=='.'){
      // 递归
      // ……
  }
  

所以，完整程序如下：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
const int inf = 101;
int n, m, ans,
	fx[5] = {0, -1, 1, 0, 0},
	fy[5] = {0, 0, 0, -1, 1};
bool a[inf][inf];
void dfs(int x, int y){
	a[x][y] = true;
	for(int i=1; i<=4; i++){
		int xx = x + fx[i],
			yy = y + fy[i];
		if(
		   xx >= 1 && xx <= n &&
		   yy >= 1 && yy <= m &&
		   !a[xx][yy]
		) dfs(xx, yy);
	}
}
int main(){
	ios :: sync_with_stdio(false);
	cin >> n >> m;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			char c;
			cin >> c;
			a[i][j] = c == '#';
		}
	}
	dfs(1, 1);
	cout << (a[n][m] ? "Yes" : "No");
	return 0;
}

另外，如果想输出路径，可以用结构体创建一个点的数据类型记录其坐标，再一个个输出。例如：

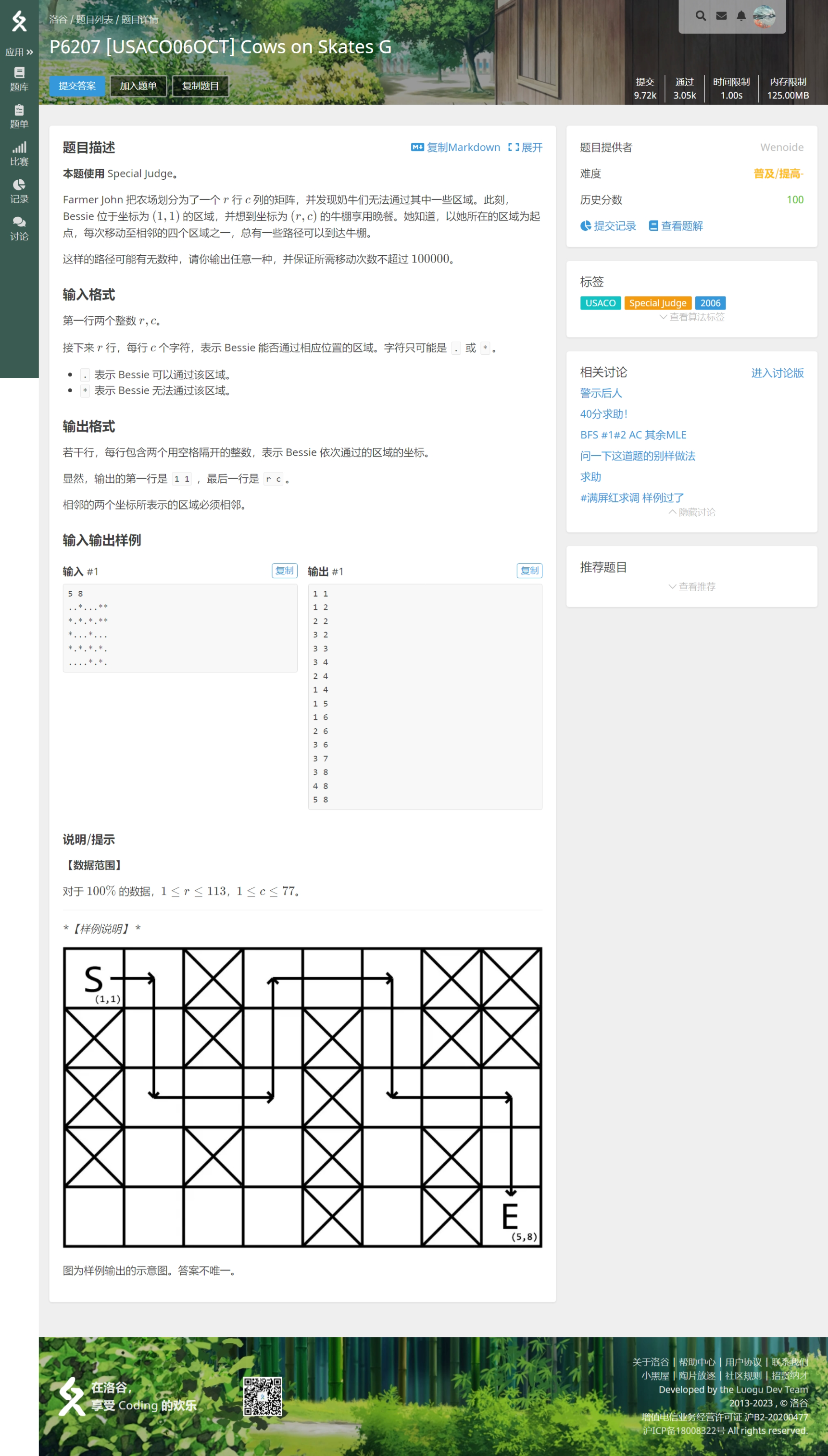
根据以往的经验，我们可以任意输出一组，就和问能否出去一样，只有一个记录路径。

那可能有人就要问了：前面的几节为什么有回溯呢？

——我们现在只需要输出一组。如果需要输出多组（所有路径），当然要回溯啦！

如果现在回溯的话，就会：

如果您的做法超时，请看：

完整程序：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

const int INF1 = 115, INF2 = 80;
struct node{
	int x, y;
} f[801];
bool a[INF1][INF2];
int r, c, fx[5] = {0, -1, 1, 0, 0}, fy[5] = {0, 0, 0, -1, 1};

void dfs(int x, int y, int st){
	a[x][y] = true;
	f[st].x = x, f[st].y = y;
	
	if(x == r && y == c){
		for(int i=1; i<=st; i++){
			cout << f[i].x << " " << f[i].y << endl; 
		}
		exit(0);
	}
	
	for(int i=1; i<=4; i++){
		int xx = x + fx[i], yy = y + fy[i];
		if(xx>=1 && xx<=r && yy>=1 && yy<=c && !a[xx][yy] && st+1<=int(1e6)+1){
			dfs(xx, yy, st + 1);
			// a[xx][yy] = false;
		}
	}
}

int main(){
	ios :: sync_with_stdio(0);
	
	memset(a, -1, sizeof(a));
	cin >> r >> c;
	for(int i=1; i<=r; i++){
		for(int j=1; j<=c; j++){
			char ch;
			cin >> ch;
			a[i][j] = !(ch == '.');
		}
	}
	dfs(1, 1, 1);
	
	return 0;
}

如下是全部路径的题，可以思考一下怎么做！

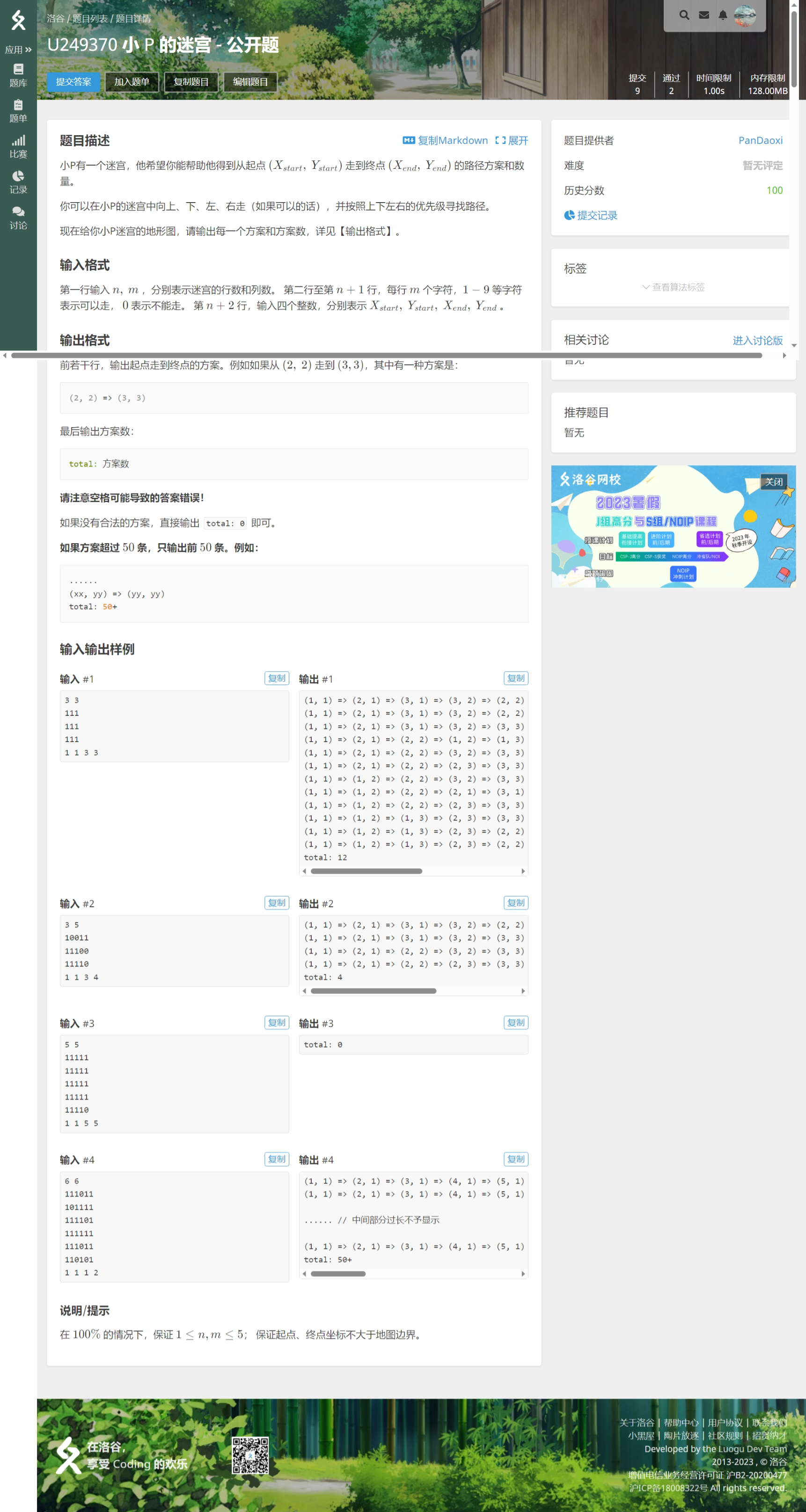
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

const int INF = 6;
int n, m, ans,
	startX, startY,
	endX, endY,
	fx[5] = {0, -1, 1, 0, 0},
	fy[5] = {0, 0, 0, -1, 1},
	p[INF*INF][3];
bool v[INF][INF];

void dfs(int x, int y, int step=1){
	if(!v[x][y]) return;

	v[x][y] = false,
	p[step][1] = x,
	p[step][2] = y;

	if(x == endX && y == endY){
		ans++;
		if(ans == 51){
			printf("total: 50+");
			exit(0);
		}

		for(int i=1; i<=step-1; i++){
			printf("(%d, %d) => ", p[i][1], p[i][2]);
		}
		printf("(%d, %d)\n", p[step][1], p[step][2]);
		return;
	}

	for(int i=1; i<=4; i++){
		int xx = x + fx[i],
			yy = y + fy[i];
		if(
			xx >= 1 && xx <= n &&
			yy >= 1 && yy <= m &&
			v[xx][yy]
		){
			dfs(xx, yy, step+1);
			v[xx][yy] = true;
		}
	}
}

int main(){
	ios :: sync_with_stdio(false);

	cin >> n >> m;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			char c;
			cin >> c;
			v[i][j] = (c != '0');
		}
	}

	cin >> startX >> startY >> endX >> endY;
	dfs(startX, startY);

	printf("total: %d", ans);
	return 0;
}

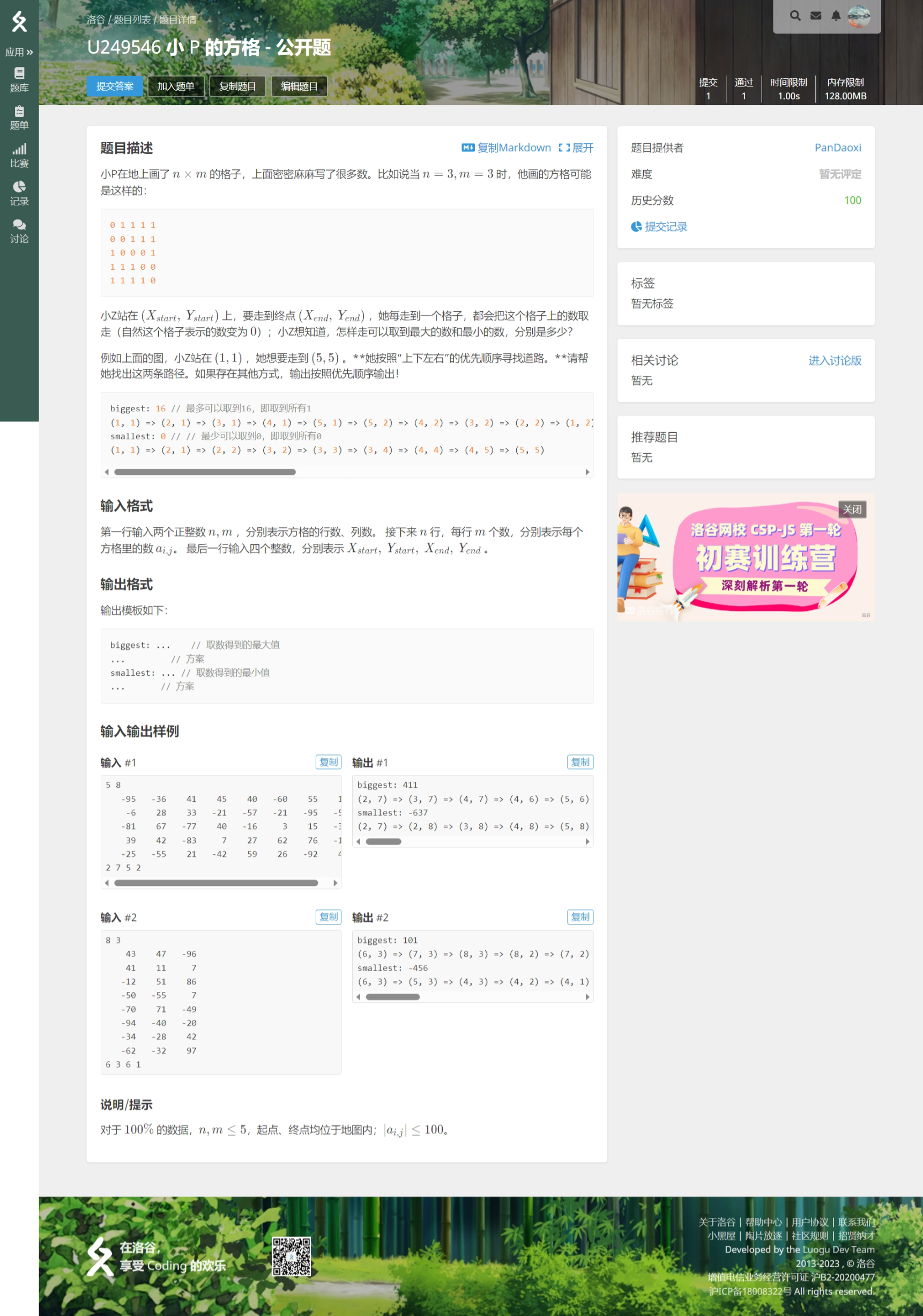
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

const int INF = 11;
int n, m, biggest, smallest,
	startX, startY, endX, endY, bigStep, smallStep,
	a[INF][INF], b[INF*INF][3], big[INF*INF][3], small[INF*INF][3],
	fx[5] = {0, -1, 1, 0, 0},
	fy[5] = {0, 0, 0, -1, 1};
bool v[INF][INF];

void dfs(int x, int y, int step=1, int res=0){
	v[x][y] = true,
	b[step][1] = x,
	b[step][2] = y,
	res += a[x][y];

	if(
		x == endX &&
		y == endY
	){
		if(res > biggest){
			biggest = res,
			bigStep = step;
			memset(big, 0, sizeof(big));
			for(int i=1; i<=step+1; i++){
				big[i][1] = b[i][1],
				big[i][2] = b[i][2];
			}
		}
		if(res < smallest){
			smallest = res,
			smallStep = step;
			memset(small, 0, sizeof(small));
			for(int i=1; i<=step+1; i++){
				small[i][1] = b[i][1],
				small[i][2] = b[i][2];
			}
		}
		return;
	}
	
	for(int i=1; i<=4; i++){
		int xx = x + fx[i],
			yy = y + fy[i];
		if(
			xx >= 1 && xx <= n &&
			yy >= 1 && yy <= m &&
			!v[xx][yy]
		){
			dfs(xx, yy, step+1, res);
			v[xx][yy] = false;
		}
	}
	
}

int main(){
	ios :: sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

	biggest = INT_MIN,
	smallest = INT_MAX;
	
	cin >> n >> m;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			cin >> a[i][j];
		}
	}
	
	cin >> startX >> startY >> endX >> endY;
	dfs(startX, startY);
	
	printf("biggest: %d\n", biggest);
	for(int i=1; i<=bigStep-1; i++){
		printf("(%d, %d) => ", big[i][1], big[i][2]);
	}
	printf("(%d, %d)\n", big[bigStep][1], big[bigStep][2]);
	
	printf("smallest: %d\n", smallest);
	for(int i=1; i<=smallStep-1; i++){
		printf("(%d, %d) => ", small[i][1], small[i][2]);
	}
	printf("(%d, %d)", small[smallStep][1], small[smallStep][2]);
	
	return 0;
}

记忆化搜索

什么是记忆化呢？

记忆化搜索 - OI Wiki (oi-wiki.org)

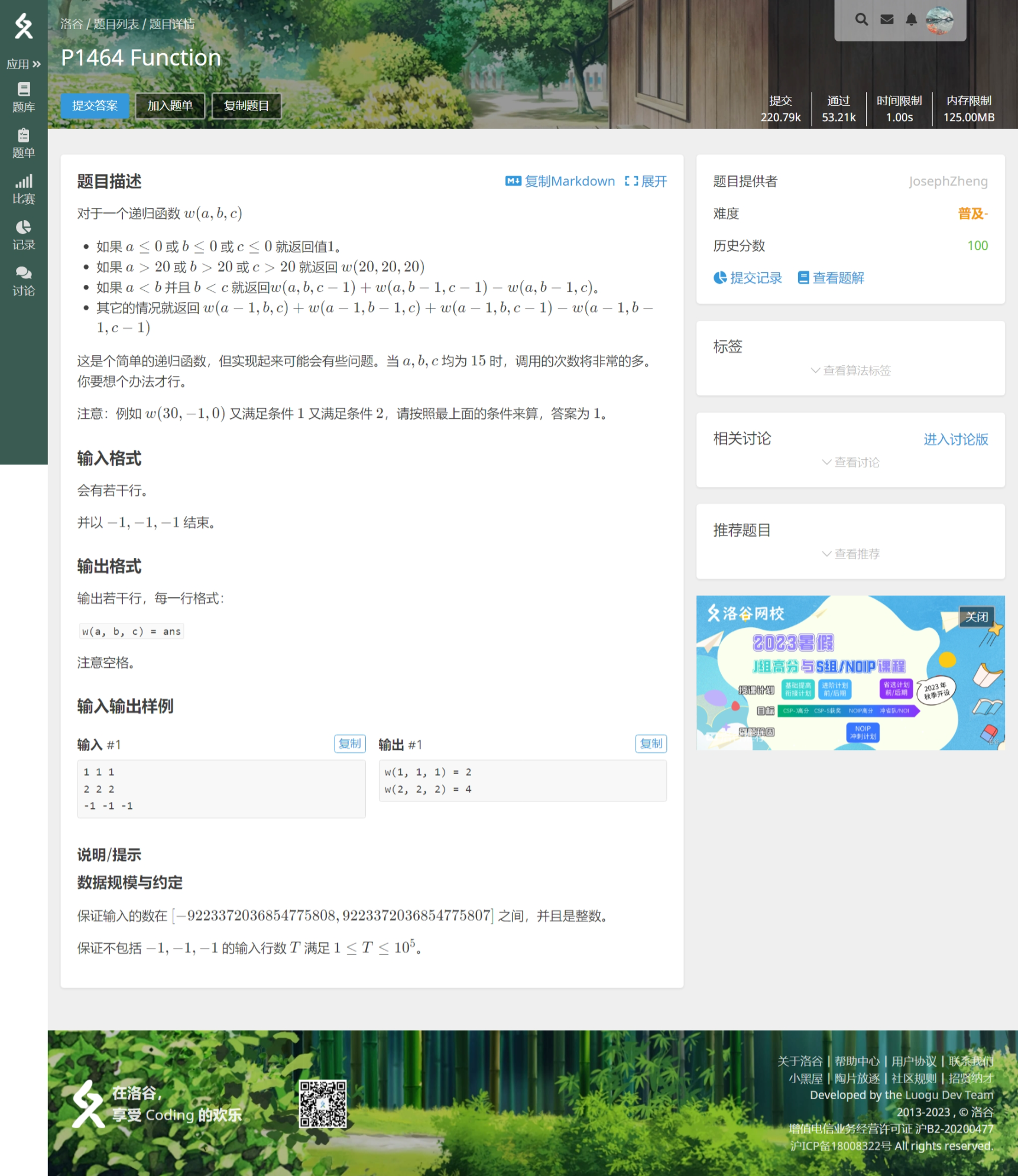
// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

#define endl "\n"
#define ll long long

const ll INF = 101;
ll x, y, z, f[INF][INF][INF];

ll w(ll a, ll b, ll c){
	if(a <= 0 || b <= 0 || c <= 0) return 1;
	else if(f[a][b][c]) return f[a][b][c];
	else if(a > 20 || b > 20 || c > 20) return f[a][b][c] = w(20, 20, 20);
	else if(a < b && b < c) return f[a][b][c] = w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c);
	else return f[a][b][c] = w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1);
}

int main(){
	ios :: sync_with_stdio(false);

	while(cin >> x >> y >> z){
		// memset(f, 0, sizeof(f));
		if(x == -1 && y == -1 && z == -1) break;
		ll tmpX, tmpY, tmpZ;
		tmpX = min(21ll, x);
		tmpY = min(21ll, y);
		tmpZ = min(21ll, z);
		
		printf("w(%ld, %ld, %ld) = %ld\n", x, y, z, w(tmpX, tmpY, tmpZ));
	}

	return 0;
}

后面会和动态规划联系在一起讲。