这大概是我第一次发绿题的题解吧……

这道题我整了好几天，才过。

题面 $\&$ 题解

如果单纯地思考怎么拿部分分，那这个题并不难，暴力模拟一遍就行了，小样例能过。
如果你要拿，那你就不能枚举了，需要二分降低时间复杂度。

我的老师说过：求最小值的最大值（最大值的最小值），跑不了二分答案。

因为起点和终点都有路标，所以我们可以确定出“空旷值”的范围啦（即下限为 $0$， 上限为 $L$）。我们在这期间开始二分答案每一个“空旷值”。

思考一下，二分答案的判断函数怎么写呢？
我们可以从第一个路标枚举到最后一个路标，取两个路标的距离差。如果这个距离差大于$mid$，那么我们就可以增加一个路标了。
为了进一步降低时间复杂度，我们可以使用小学数学来解决一下。我们可以知道：

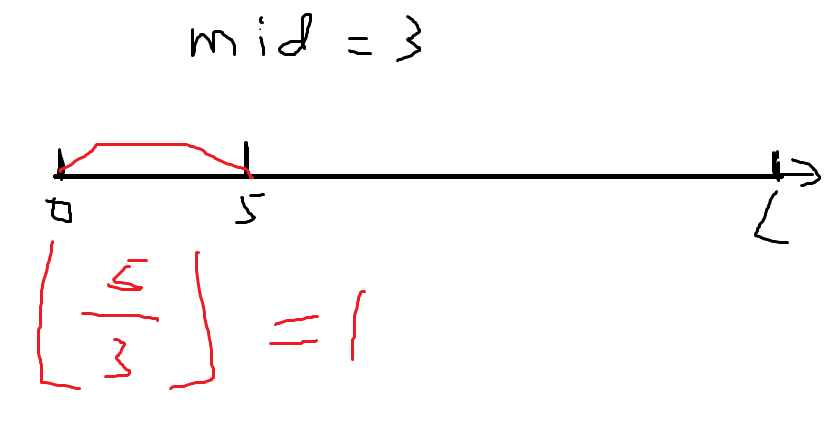
（图画的很丑，拿鼠标画的我尽力了）
考虑一种特殊情况，如果距离差刚好整除$mid$，那么需要减去一。

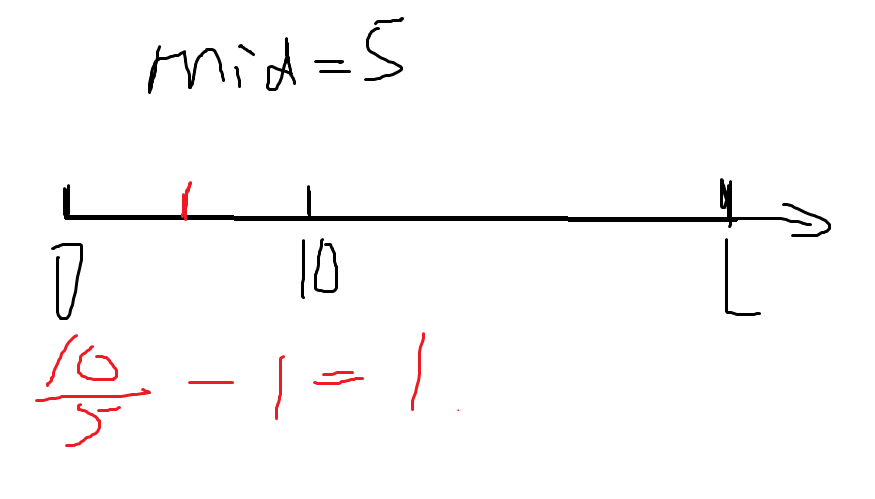
我们用一个计数器$cnt$记录每一个距离差之间放的路标数量。我们可以根据$cnt$和最多放的路标数量$K$作比较，如果$cnt<=K$返回真，反之返回假。

再说二分模板，我们可以根据$check$函数的返回值来对应$l$和$r$的变化。如果返回值为真，说明空旷值还可以进一步缩小；反之表示空旷值过小。
因此如果$check$返回真，我们需要往左看；返回假，我们需要向右看。

由于最后是求最小值，所以需要输出左边界。

完整程序如下：

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;

const int INF = 1e5 + 1;
int k, n, m, l, r, mid, a[INF];

bool check(int t){
	int cnt = 0,
		now = 0;
	for(int i=1; i<=n; i++){
		/*
            取两个路标之差x，cnt+=x/t
            特判如果x%t为0，那么cnt--
		*/
  		now = a[i] - now;
		if(now > t) cnt += now/t - (now%t == 0);
		now = a[i];
	}
	if(cnt <= m) return true;
	else return false;
}

int main(){
	ios :: sync_with_stdio(false);

	cin >> k >> n >> m;
	for(int i=1; i<=n; i++){
		cin >> a[i];
	}
	l = 0, r = k;

	while(l <= r){
		mid = (l+r) / 2;
		if(check(mid)){
			r = mid - 1;
		}
		else{
			l = mid + 1;
		}
	}
	cout << l;

	return 0;
}

拓展

Luogu P2678 跳石头

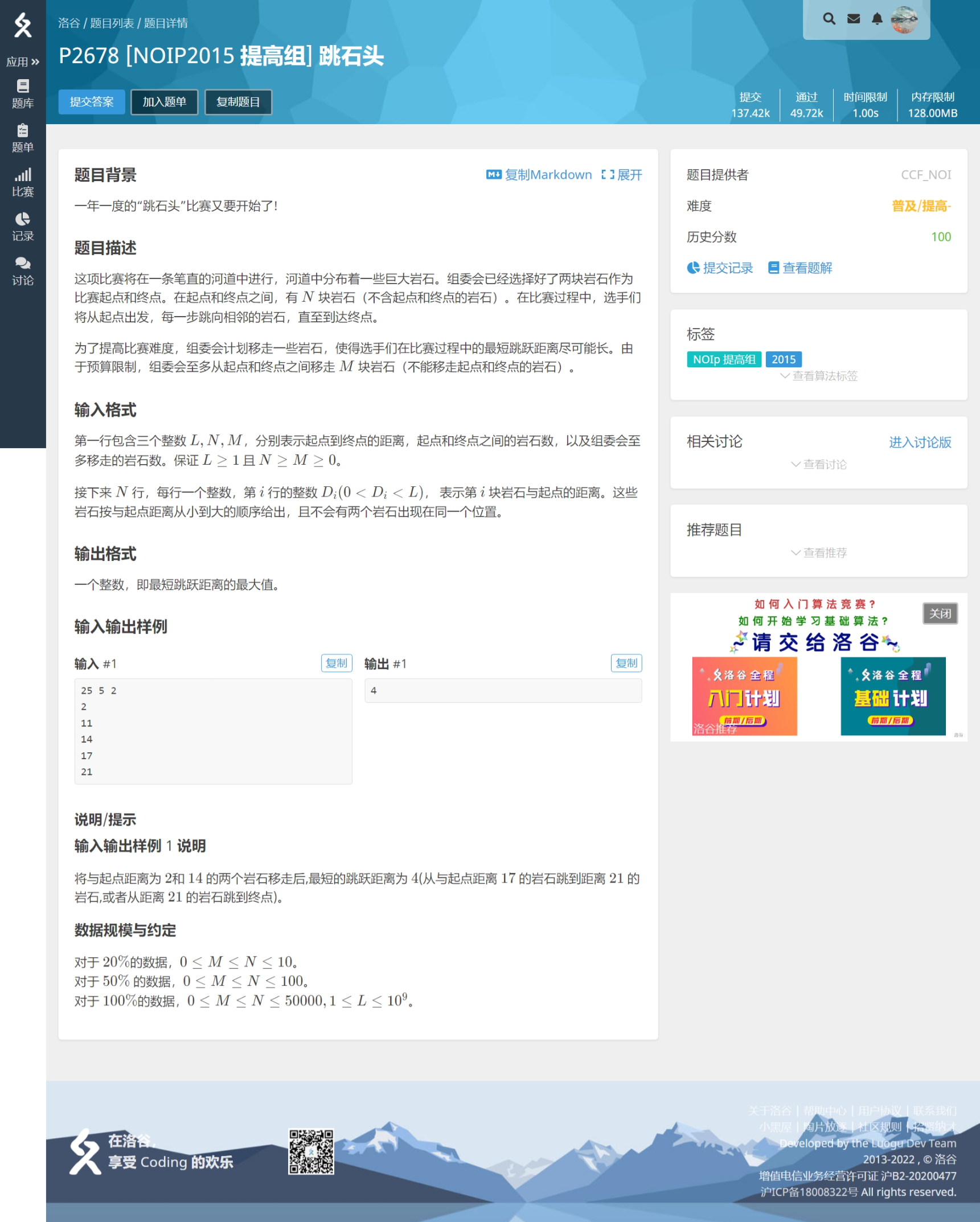
类比于《路标设置》的思想，刚才的那道题是枚举空旷指数，这个题是枚举跳跃距离。思考一下，得到以下程序：

// Author:PanDaoxi
#include <bits/stdc++.h>
#define int long long
using namespace std;

const int INF = 5e4 + 1;
int k, m, n, l, r, mid, a[INF];

bool check(int t){
	int cnt = 0,
		now = 0;
	for(int i=1; i<=n; i++){
		if(a[i] - now >= t) now = a[i];
		else cnt++;
	}
	if(k - now < t){
		cnt++;
	}
	if(cnt <= m) return true;
	else return false;
}

signed main(){
	ios :: sync_with_stdio(false);
	
	cin >> k >> n >> m;
	l = 1, r = k;
	for(int i=1; i<=n; i++){
		cin >> a[i];
	}

	while(l <= r){
		mid = (l+r) / 2;
		if(check(mid)){
			l = mid + 1;
		}
		else{
   			r = mid - 1;
		}
	}
	cout << r;
	
	return 0;
}

题外话

预祝全天下$OIer$们程序员节快乐！

我去年$1024$来的洛谷，到今天快一年了。

一年前我还啥也不是，现在已经可以开始挑战难题了（部分是跟着老师做的）

由于今年的形势（学校那边的七天小长假不好请），我决定不参加$CSP2022$，再努力一年，明年再战。
$OIer$们加油啊！祝全天下$OIer$能取得好成绩！