分享笑话一则：洛谷神图

树是啥？不就是树吗？

实际上，我们今天所说的树，是一种数据结构。
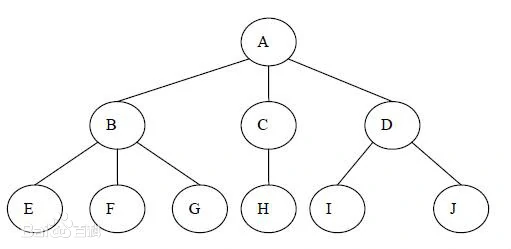
它叫做树形结构，实际上长这样：

树

今天的概念比较多，也很繁杂，大家看看就行，没必要完全记住，只要知道大概的意思即可。

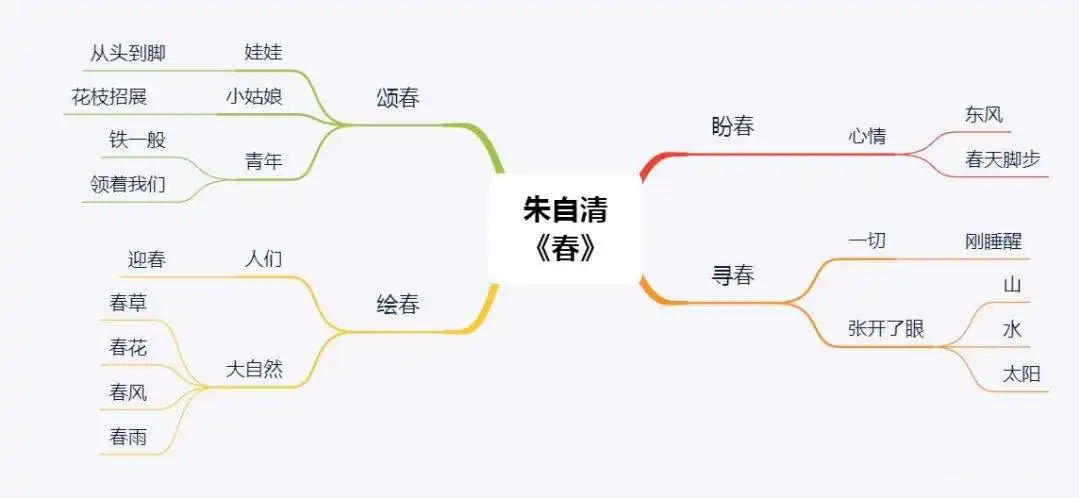
对于树，大家见得比较多的是思维导图。其实这是一种树。
在这里插入图片描述
还有目录树。比如下面这个（这是我自己开发的一款小软件)：

D:.
│  db.sqlite3
│  main.py
│  manage.py
│  README.md
│  TTS_config
│
├─About
│  │  依赖包安装工具.bat
│  │
│  └─Update
│          EMERGENCY.md
│          README.md
│
├─Client
│      Client.py
│      VERSION
│
└─VeryControl
    │  asgi.py
    │  settings.py
    │  urls.py
    │  VERSION
    │  wsgi.py
    │  __init__.py
    │
    └─__pycache__
            settings.cpython-36.pyc
            urls.cpython-36.pyc
            wsgi.cpython-36.pyc
            __init__.cpython-36.pyc

我们将其抽象化，就形成了树形结构。

树的概念

结点

我们将以这棵树为例来讲解下面的几个概念。
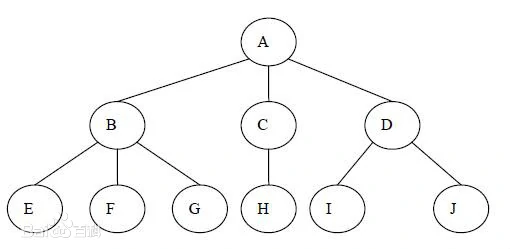
在这里插入图片描述
注意别写错字，是“结点”而非“节点”。
像上图中那样， $A,\ B,\ C$ 等都称作结点。
其中，一棵树最开始的分支，比如上图中的结点 $A$ ，叫做根结点。

注意嗷，有些结点下面的分支还指向其他的结点（例如结点 $B$ ），那么我们称分支下来的结点为孩子（如结点 $E,\ F,\ G$ ）；

如果站在结点 $E$ 的角度看结点 $B$ ，则称结点 $B$ 为结点 $E$ 的双亲，结点 $A,\ B$ 是结点 $E$ 的祖先；反之，如果我站在根节点看下面的所有结点，那么称这些结点为子孙结点。

同一结点的孩子结点，我们称这些结点为兄弟；不同结点但是层数相同的孩子结点，我们称这些结点为堂兄弟。

我们知道，每一个结点都可能有孩子结点。如果有一个结点没有孩子结点，那么我们称这个结点为叶子结点。

度、层数、高度、子树

对于任意一个结点，度指这个结点有几个孩子结点。
例如下面这棵树，结点 $E$ 的度为 $2$ ；结点 $A$ 的度为 $3$ 。
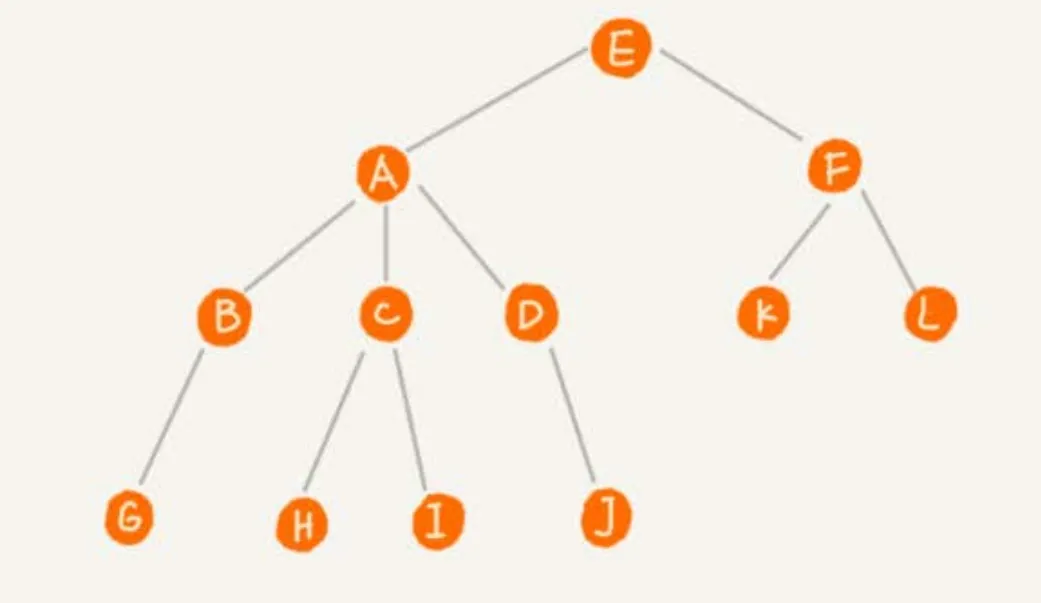
在这里插入图片描述
那么，对于一棵树的度，指各个子结点的度的最大值。例如上面的那棵树的度就为 $3$ ，因为 $A$ 结点有 $3$ 个孩子结点。

层数很好理解，比如说 $E$ 在第一层， $A,\ F$ 在第二层， $B,\ C,\ D,\ K,\ L$ 在第三层……

高度指某棵树的最大延伸长度。这棵树的高度为 $3$ ，因为它延伸了 $3$ 层。
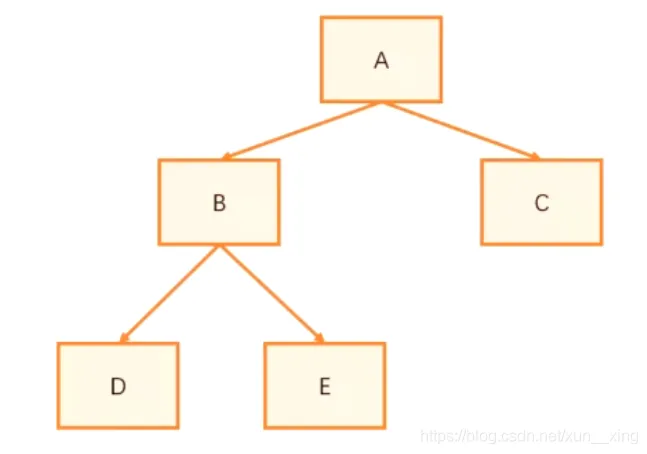
在这里插入图片描述

子树是什么？子树其实就是某棵树的一部分。例如：
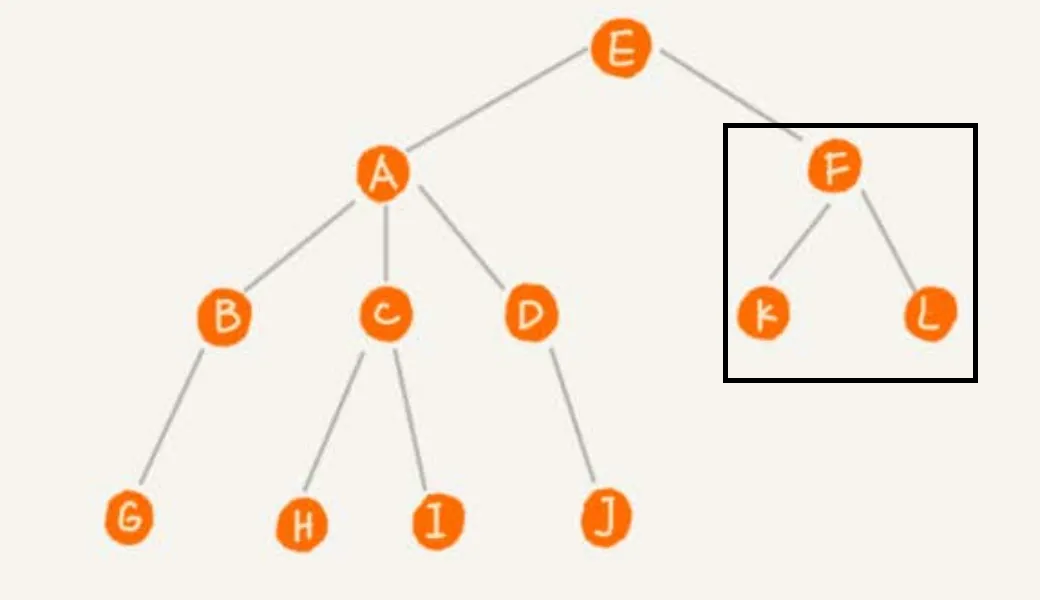
在这里插入图片描述
其中画黑框的就是整棵树的一个子树。

独根树、满树、完全树

独根树应该不难理解吧：这棵树只有一个结点，即根结点。

满树，即一棵树的所有结点（除了最后一层的叶子结点）的度均相等。
例如，这就是一棵满树，它的度数为 $2$ ：
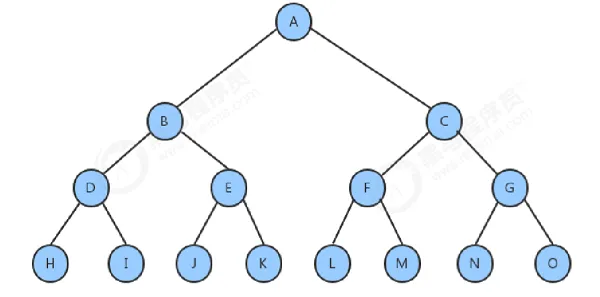
在这里插入图片描述
完全树：完全树是指从根节点开始，由上至下，从左到右，一个个地给结点标号。直到标到最后的的叶子结点。如果某一编号的结点与满树的位置相同，则这是一棵完全树。
如下图，这是一棵完全树。
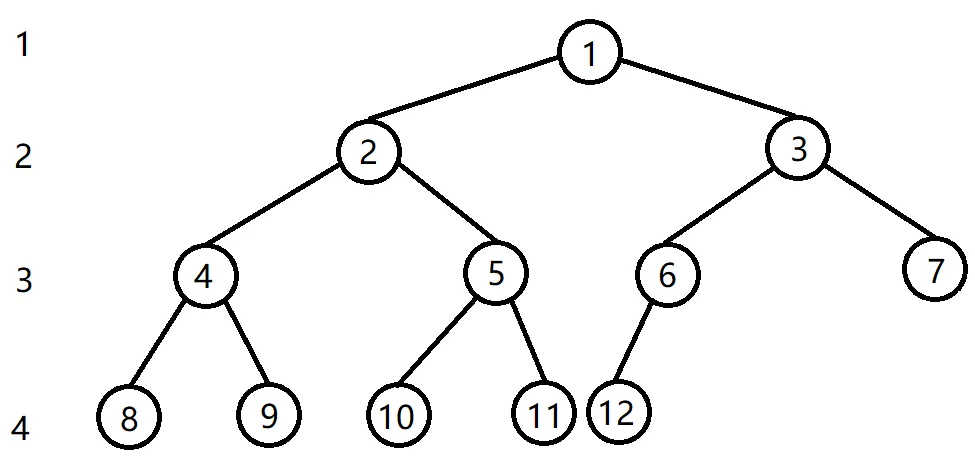
在这里插入图片描述
有没有感觉太恐怖了？！

至于最优二叉树（哈夫曼树)、红黑树、二叉平衡树、对称二叉树等，我们以后再讲。

二叉树

恭喜你，你已经完成一半的任务了。
我们来看看二叉树。

先说二叉树是什么：二叉树是度为 $2$ 的树。
二叉树是比较特殊的一种树。它大概长这样：
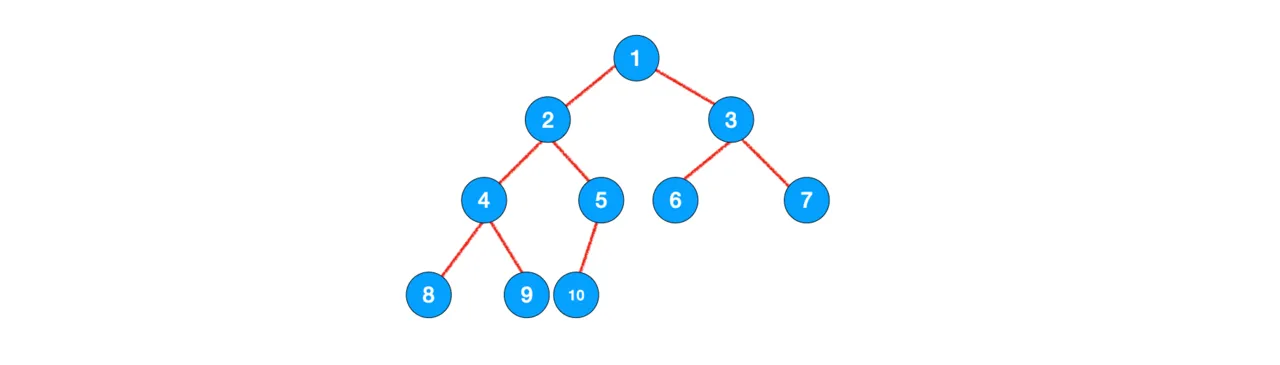
在这里插入图片描述
其中，一个度为 $2$ 的结点，它的两个孩子结点分别叫做左孩子、右孩子。

遍历

学二叉树，我们跑不了二叉树遍历。
二叉树遍历主要分 $3$ 种，分别是：

先序遍历
中序遍历
后序遍历

这三种遍历，我们来看看如何实现吧！

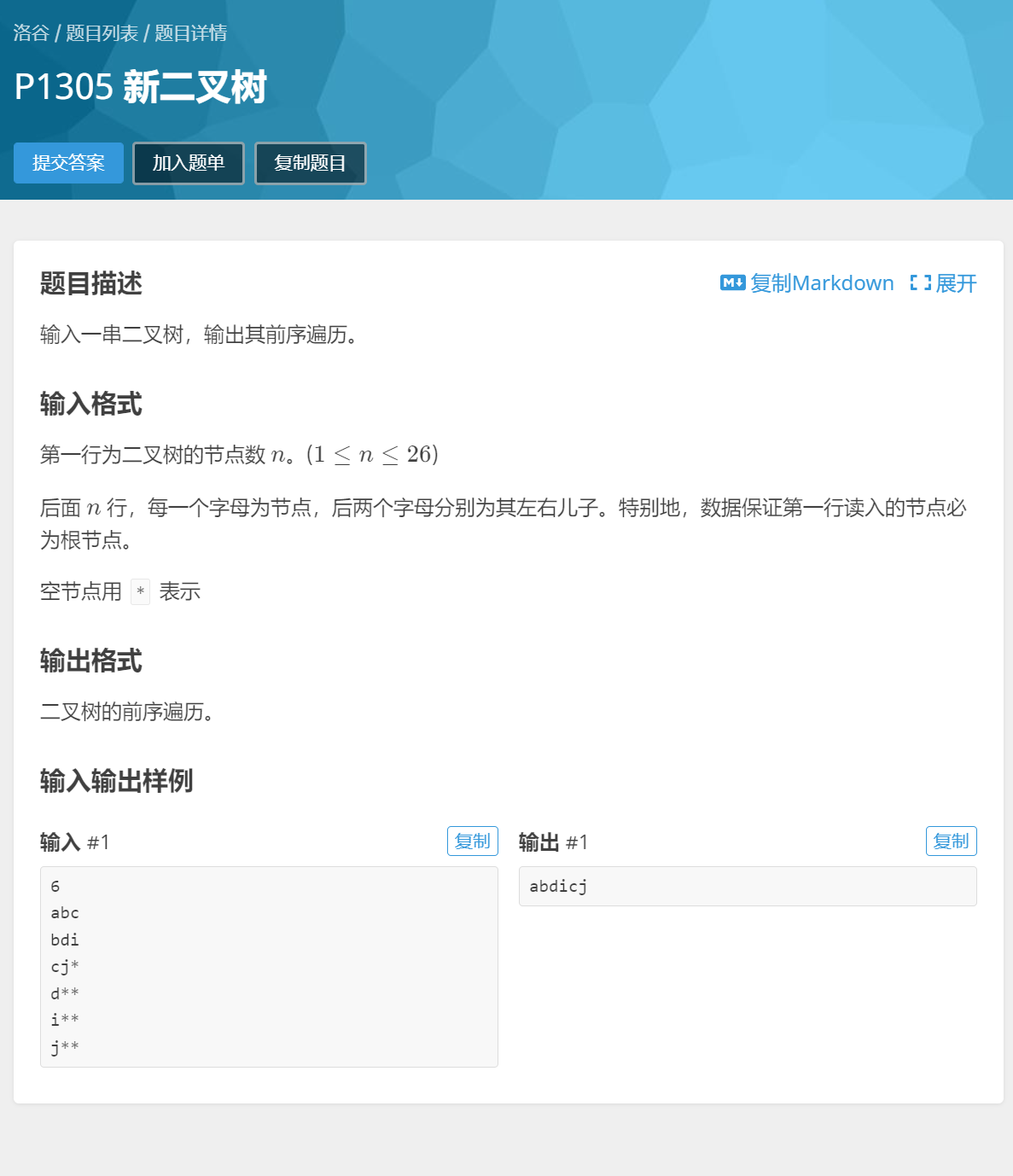
先序遍历

先序遍历的口诀是“根左右”，意为先遍历根节点，然后是以左孩子为根节点遍历子树，直到叶子结点再回溯遍历右孩子结点的子树。

我们看到了“回溯”，应该能想起来点什么吧？
——递归。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
map <char, string> tree; // 映射字典，我们可以通过一个字符来获取它的左右孩子
int n;
void f(char root){
    if(root == '*') return; // 跳出递归
    cout << root; // 输出根节点
    f(tree[root][0]); // 遍历以左孩子为根节点的子树
    f(tree[root][1]); // 遍历以右孩子为根节点的子树
}
int main(){
    char root;
    cin >> n;
    for(int i=1; i<=n; i++){
        char a, b, c;
        cin >> a >> b >> c;
        if(i == 1) root = a; // 记录整棵树的根节点
        tree[a] = string(1, b) + string(1, c); // 字符串拼接
    }
    f(root); // 从整棵树的根节点开始递归遍历
    return 0;
}

中序遍历

同样的道理，但是中序遍历的口诀是“左根右”。即先访问左孩子，再访问根结点，最后是右孩子。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
map <char, string> tree; // 映射字典，我们可以通过一个字符来获取它的左右孩子
int n;
void f(char root){
	if(root == '*') return; // 跳出递归
	f(tree[root][0]); // 遍历以左孩子为根节点的子树
	cout << root; // 输出根节点
	f(tree[root][1]); // 遍历以右孩子为根节点的子树
}
int main(){
	char root;
	cin >> n;
	for(int i=1; i<=n; i++){
		char a, b, c;
		cin >> a >> b >> c;
		if(i == 1) root = a; // 记录整棵树的根节点
		tree[a] = string(1, b) + string(1, c); // 字符串拼接
	}
	f(root); // 从整棵树的根节点开始递归遍历
	return 0;
}

在这里插入图片描述
以这棵树为例，我们从最左边开始，遍历顺序为：

A -> B -> D -> B -> E -> A -> C 
          -    -    -    -    -

所以遍历结果为 $DBECA$ 。

后序遍历

后序遍历的口诀为“左右根”，即最后输出根节点。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
map <char, string> tree; // 映射字典，我们可以通过一个字符来获取它的左右孩子
int n;
void f(char root){
	if(root == '*') return; // 跳出递归
	f(tree[root][0]); // 遍历以左孩子为根节点的子树
	f(tree[root][1]); // 遍历以右孩子为根节点的子树
	cout << root; // 输出根节点
}
int main(){
	char root;
	cin >> n;
	for(int i=1; i<=n; i++){
		char a, b, c;
		cin >> a >> b >> c;
		if(i == 1) root = a; // 记录整棵树的根节点
		tree[a] = string(1, b) + string(1, c); // 字符串拼接
	}
	f(root); // 从整棵树的根节点开始递归遍历
	return 0;
}

在这里插入图片描述
同样是这棵树，那么遍历顺序应该是：

A -> B -> D -> E -> B -> C -> A
          -    -    -    -    -

所以遍历结果为 $DEBCA$ 。

拓展

放几道稍难点的题，给大家看。

给出中序、后序遍历求先序遍历

首先，单单给出中序或后序是求不出来二叉树的，因为有不同的形态。但是先序和中序同时出现而且合法，就能求出唯一二叉树。

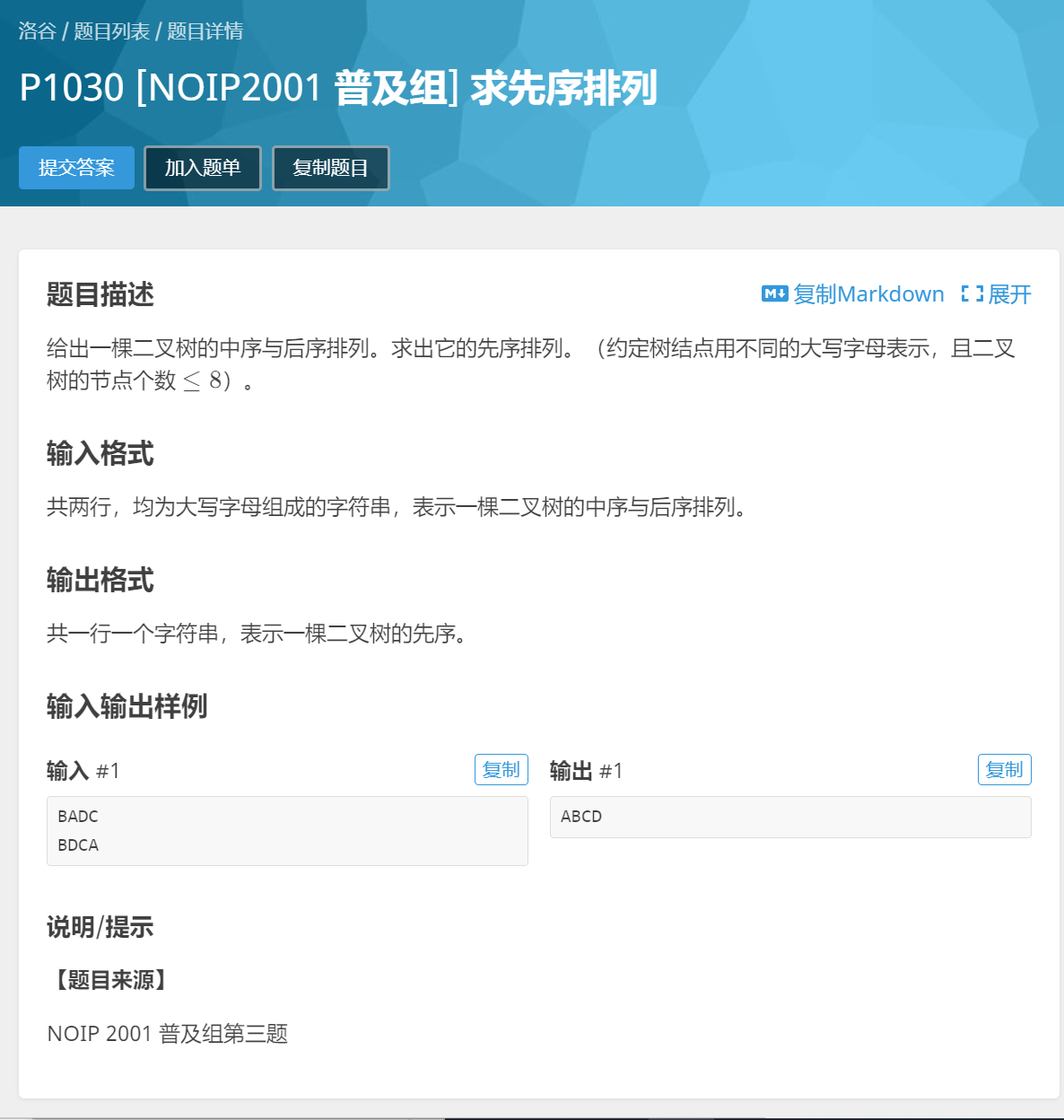
在这里插入图片描述
这个题目的切入点是什么？
——后序遍历。后序遍历的最后一位，永远是二叉树的根节点。

找到根节点以后干嘛呢？中序遍历里面，根节点前面的全都是第二层左孩子的子树，后面全都是第二层右孩子的子树。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
void f(string s1, string s2){
	if(!s1.size()) return;
	char c = s2[s2.size()-1];
	cout << c;
	int t = s1.find(c); // 找到中序遍历里面根的下标
	f(s1.substr(0, t), s2.substr(0, t)); // 遍历左子树
	f(s1.substr(t+1), s2.substr(t, s2.size()-t-1));
}
int main(){
	string a, b;
	cin >> a >> b;
	f(a, b);
	return 0;
}

给出先序、中序遍历，求后序遍历

在这里插入图片描述
切入点就是，先序遍历的第一个字符即为二叉树的根结点。

// Author:PanDaoxi
#include <bits/stdc++.h>
using namespace std;
void f(string s1, string s2){
	if(!s2.size()) return;
	char c = s2[0];
	int t = s1.find(c);
	f(s1.substr(0, t), s2.substr(1, t));
	f(s1.substr(t+1), s2.substr(t+1));
	cout << c;
}
int main(){
	string a, b;
	cin >> a >> b;
	f(a, b);
	return 0;
}

PanDaoxi's Tech Blog

八、树形数据结构

树